算法——所有节点对的最短路径:Floyd-Warshall算法、Johnson算法
前言
前面介绍了单源最短路径问题,本文是介绍所有节点对的最短路径问题,首先我们会想到用前面所介绍的知识来求解该问题,根据不同类型的图可以用一下几种方法求解:
- 若无权重的图,则可以使用
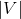 次BFS,时间复杂度是
次BFS,时间复杂度是 ;
; - 若为非负权重边的图,则可以使用
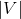 次Dijkstra算法,不同的优先队列实现得到不同的时间复杂度:①线性数组,
次Dijkstra算法,不同的优先队列实现得到不同的时间复杂度:①线性数组,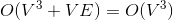 。②二叉堆,
。②二叉堆,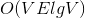 ,在稀疏图的情况下是一个较大的改进。③斐波那契堆,
,在稀疏图的情况下是一个较大的改进。③斐波那契堆, ;
; - 若含有负权重边的图,则可以使用
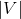 次Bellman-Ford算法,稠密的情况下时间复杂度是为
次Bellman-Ford算法,稠密的情况下时间复杂度是为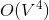 ;
;
Floyd-Warshall算法
该算法的原理是动态规划,并且图![]() 的表示方式是邻接表矩阵。根据动态规划的求解步骤:
的表示方式是邻接表矩阵。根据动态规划的求解步骤:
- 分析最优解结构;
- 递归定义最优解的值;
- 自底向上计算最优解的值;
- 根据计算出的最优解的值构造最优解;
使用该算法是可以存在负权值的边,但不能存在权值为负值的环路。在求解之前先介绍基本概念:
中间节点:简单路径![]() 的中间节点是指路径
的中间节点是指路径![]() 上除节点
上除节点![]() 和节点
和节点![]() 之外的任意节点,也就是处于集合
之外的任意节点,也就是处于集合![]() 中的节点。
中的节点。
Floyd-Warshall算法的求解步骤:
最短路径结构(最优解结构)
假定图![]() 的所有节点为
的所有节点为![]() ,考虑其中一个子集
,考虑其中一个子集![]() ,
,![]() 的某个整数。对任意节点
的某个整数。对任意节点![]() ,考虑从节点
,考虑从节点![]() 到节点
到节点![]() 的所有中间节点均取自集合
的所有中间节点均取自集合![]() 的路径,并且设
的路径,并且设![]() 为其中权重最小的路径。Floyd-Warshall算法利用路径
为其中权重最小的路径。Floyd-Warshall算法利用路径![]() 和从节点
和从节点![]() 到节点
到节点![]() 之间中间节点均取自集合
之间中间节点均取自集合![]() 的最短路径之间的关系。该关系依赖于节点
的最短路径之间的关系。该关系依赖于节点![]() 是否是路径
是否是路径![]() 上的一个中间节点。
上的一个中间节点。
- 若节点
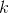 不是路径
不是路径 的中间节点,则路径
的中间节点,则路径 上的中间节点都属于集合
上的中间节点都属于集合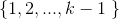 。因此,从节点
。因此,从节点 到节点
到节点 之间中间节点均取自集合
之间中间节点均取自集合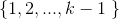 的一条最短路径也是从节点
的一条最短路径也是从节点 到节点
到节点 的所有中间节点均取自集合
的所有中间节点均取自集合 的一条最短路径,即:
的一条最短路径,即: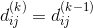 ,其中
,其中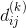 表示从节点
表示从节点 到节点
到节点 的所有中间节点均取自集合
的所有中间节点均取自集合 的一条最短路径的权重。
的一条最短路径的权重。 - 若节点
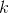 是路径
是路径 的中间节点,则将路径
的中间节点,则将路径 分解为
分解为 ,因此,
,因此, 是从节点
是从节点 到节点
到节点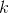 之间中间节点均取自集合
之间中间节点均取自集合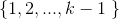 的一条最短路径,,
的一条最短路径,,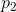 是从节点
是从节点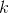 到节点
到节点 之间中间节点均取自集合
之间中间节点均取自集合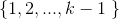 的一条最短路径,即:
的一条最短路径,即: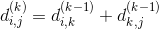
最短路径的一个递归解(递归定义最优解的值)
根据上面的分析可得一个递归解:
自底向上计算最短路径的权重
根据递归公式计算出最短路径权重。计算伪代码如下:
FLOYD-WARSHALL(W)
{
n = W.rows;
D(0) = W;
for(k = 1;k <= n;++k){
let D(k) = d[i,j](k) be a new n*n matrix;
for i = 1 to n
for j = 1 to n
d[i,j](k) = min(d[i,j](k-1), d[i,k](k-1)+ d[k,j](k-1) )
}
return D(n);
}
构造一条最短路径
我们选择在计算最短路径权值矩阵的![]() ,同时计算前驱矩阵
,同时计算前驱矩阵![]() ,我们定义
,我们定义![]() 为从节点
为从节点![]() 到节点
到节点![]() 之间中间节点均取自集合
之间中间节点均取自集合![]() 的最短路径上
的最短路径上![]() 的前驱节点。
的前驱节点。![]() 的递归定义跟最短路径权重类似。
的递归定义跟最短路径权重类似。
当![]() 时:
时:
当![]() 时:
时:
计算过程只是在计算最短路径权重的基础上加上计算前驱矩阵的算法即可。伪代码如下:
FLOYD-WARSHALL(W)
{
n = W.rows;
D(0) = W;
TT(0) = 初始值
for(k = 1;k <= n;++k){
let D(k) = d[i,j](k) be a new n*n matrix;
let TT(k) = π[i,j](k) be a new n*n matrix;
for i = 1 to n
for j = 1 to n
d[i,j](k) = min(d[i,j](k-1), d[i,k](k-1)+ d[k,j](k-1) )
if d[i,j](k)== d[i,j](k-1)
π[i,j](k) = π[i,j](k-1)
else π[i,j](k) = π[k,j](k-1)
}
return D(n),TT(n);
}
Johnson算法
Johnson算法主要用于求稀疏图上的所有节点对的最短路径。其主体思想是利用重新赋予权值的方法把一个原问题带负权的图转化为权值非负的图。然后再对每个节点使用一次Dijkstra算法以求出所有节点对的最短路径。时间复杂度![]() ;
;
重新赋予权值必须满足一下两个条件:
- 对于所有节点对
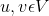 ,一条路径
,一条路径 是在使用权值函数
是在使用权值函数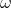 时从节点
时从节点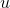 到节点
到节点 的一条最短路径,当且仅当
的一条最短路径,当且仅当 是在权值函数
是在权值函数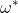 时从节点
时从节点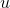 到节点
到节点 的一条最短路径。
的一条最短路径。 - 对于所有的边
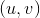 ,新的权值
,新的权值 为非负值。
为非负值。
重新赋予权值不会改变最短路径,对于每条边![]() ,权值函数的关系为:
,权值函数的关系为:![]() ,其中
,其中![]() 为新添加节点
为新添加节点![]() 到节点
到节点![]() 的最短路径;
的最短路径;
Johnson算法的步骤:
- 在带有权重的有向原始图
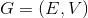 添加一个新节点
添加一个新节点 使其成为新的图
使其成为新的图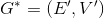 ,其中
,其中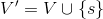 ,
, 对于原图的所有节点
对于原图的所有节点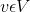 ,使其到新节点的边权值为0,即
,使其到新节点的边权值为0,即 ;
; - 用Bellman-Ford算法检查所输入的图
 是否包含权值为负的环路,若有打印不存在最短路径并退出,否则继续;
是否包含权值为负的环路,若有打印不存在最短路径并退出,否则继续; - Bellman-Ford算法计算新节点
 到所有节点
到所有节点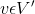 的最短路径,所计算的节点最短路径就是
的最短路径,所计算的节点最短路径就是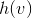 的值;
的值; - 更新所有边
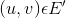 的权值,即计算
的权值,即计算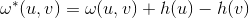 ;
; - 对已更新权值的图
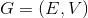 的每个节点进行一次Dijkstra算法,求出所有节点对的最短路径;
的每个节点进行一次Dijkstra算法,求出所有节点对的最短路径;
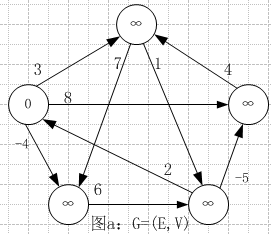
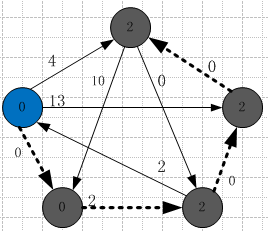
举例说明Johnson算法的实现步骤:若要计算图![]() 的所有节点对的最短路径;
的所有节点对的最短路径;
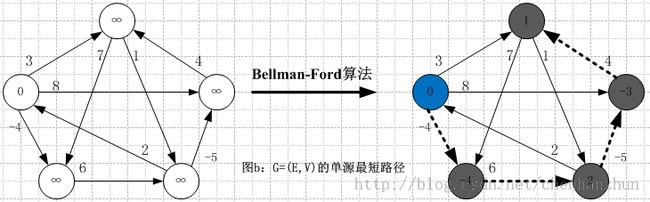
若是直接按照Bellman-Ford算法计算某个节点的最短路径,则如下图所示:
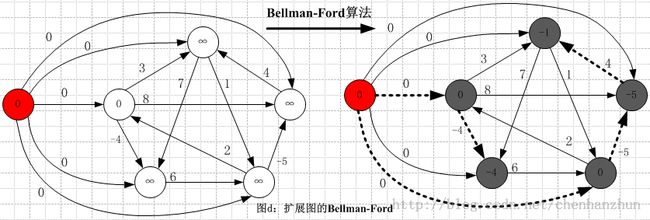
根据Johnson算法的步骤,首先添加新节点![]() 使其成为新图
使其成为新图![]() ,如下图所示:
,如下图所示:
对扩展图![]() 进行一次Bellman-Ford算法处理,得到以
进行一次Bellman-Ford算法处理,得到以![]() 为源节点的最短路径,如下图所示:
为源节点的最短路径,如下图所示:
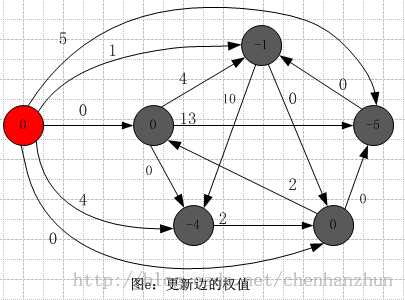
根据上一步骤以![]() 为源节点的最短路径更新边的权值,按照公式:
为源节点的最短路径更新边的权值,按照公式:![]() 进行更新,如下图所示:
进行更新,如下图所示:
根据上一步骤更新边的权值,得到新权值的图![]() ,如下图所示:
,如下图所示:
对更新权值后的图的每个节点进行一次Dijkstra算法,即可求得所有节点对的最短路径;由于只是重复的过程,下图只给出其中一个节点的求解图,其他节点这里就不给出了;提示:这里节点![]() 里面标记的权值是
里面标记的权值是![]() ,与原图最短路径的关系为:
,与原图最短路径的关系为:![]()