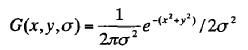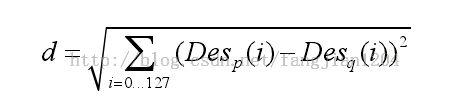sift算法
SIFT算法的实现
学习过程:一幅图像SIFT特征向量的生成算法总共包括4步:
1、检测尺度空间极值点,初步确定关键点位置和所在尺度。
2、抽取稳定的关键点,精确确定关键点的位置和尺度,同时去除低对比度的关键点和不稳定的边缘响应点,以增强匹配稳定性、提高抗噪声能力。
3、为每个关键点指定方向参数,使算子具备旋转不变性。
4、关键点描述子的生成,即生成SIFT特征向量。
匹配过程:当一幅图像的特征向量库生成后,即已经学习好之后,使用特征点匹配算法进行图像的匹配。
学习过程
基本思想:找到不同尺寸上的特征点,并为它分配一个方向,则特征点坐标、尺度大小和方向三个参数构成一个特征区域,然后根据这个特征区域求得一个特征向量,这样一幅图像就可以用若干特征向量来表示。
1、检测尺度空间极值点,初步确定关键点位置和所在尺度。
1.1、尺度空间的生成
尺度空间的详细描述见上一篇博客
提取尺度不变的特征点,其主要思想是提取的特征点出现在任何一个尺度上。这样不论图像的尺度如何变化,总能够提取出这种特征点。检测尺度无关的特征点可以通过搜索所有可能的尺度,这可以基于尺度空间理论来解决。前面已经提到,在一些合理的假设之下,高斯函数是得到图像尺度空间唯一可用的核函数。将图像 I ( x, y ) 的尺度定义为一个函数 L ( x, y , σ ) ,它由高斯函数 G ( x, y , σ )和图像 I ( x, y )卷积
得到:L ( x, y , σ ) =G ( x, y , σ ) * I ( x, y )
为了在尺度空间中高效的检测稳定关键点的位置,提出了在高斯差分函数与图像卷积得到的空间 D ( x, y , σ )中寻找极值点(其中,相邻两个尺度由一个常数 k分开):
D ( x , y , σ ) = ( G ( x , y , kσ ) - G ( x , y , σ ) ) * I ( x , y )= L ( x , y , kσ ) - L ( x , y , σ )。
高斯拉普拉斯LoG金字塔
高斯拉普拉斯LoG金字塔自下而上分为多层,在第一层中,对原始图像不断用高斯函数卷积,得到一系列逐渐平滑图像。在这一层中,相邻的高斯图像差分得到高斯差分图像。这一组进行完毕后,从中抽取一幅图像 A 进行降采样,得到图像 B的面积变为 A的 1/4,并将 B作为下一层的初始图像,重复第一层的过程。选取 A的原则是,得到 A所用的尺度空间参数 σ为本层尺度空间参数的 2倍。如图 5所示:
1.2、计算极值点
如图7,每个点最多需要和26个点进行比较。有一个问题是到底要在多少个尺度中寻找极值点,即如何确定 s 值。实验表明,s取 3是较好的选择。如果 s = 3,则需要 5幅高斯差分图像才可以。这里的计算是高效的,因为大多数情况下,只需要几步比较,就可以排除一个像素点,认为它不是极值。
2、抽取稳定的关键点,精确确定关键点的位置和尺度,同时去除低对比度的关键点和不稳定的边缘响应点,以增强匹配稳定性、提高抗噪声能力。
具体见sift中文.pdf中描述。
3、为每个关键点指定方向参数,使算子具备旋转不变性。
具体见sift中文.pdf中描述。
4、关键点描述子的生成,即生成SIFT特征向量。
前面已经为关键点赋予了图像位置、尺度以及方向,这三个参数称为一个特征区域,这一步将根据关键点周围的局部特性计算一个特征描述子,即一个特征向量。这个描述子还需要对仿射变换、光照变换等具有一定的鲁棒性。
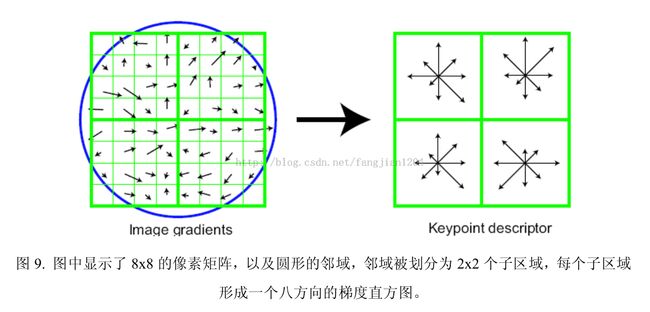
首先将坐标轴旋转为特征点的方向,以保证旋转不变性;接下来以特征点为中心取8x8的窗口(特征点所在的行和列不取)。在图9左边所示中,中央黑点为当前特征点的位置,每一个小格代表特征点所在尺度空间的一个像素,箭头方向代表该像素的梯度方向,肩头长度代表梯度模值,图中圈内代表高斯加权的范围(越靠近特征点的像素,梯度方向的信息贡献越大)。然后在4x4的图像小块上计算8个方向的梯度值直方图,绘制每个方向的累加值,形成一个种子点,如图9右侧所示。此图中一个特征点由4个种子点组成,每个种子点有8个方向向量信息,共生成32个数据,所以形成32维的SIFT特征向量即特征描述符。这种领域方向性信息联合的思想增强了算法抗噪声的能力,同时对于含有定位误差的特征匹配也提供了较好的容错性。
实际计算过程中,为了增强匹配的稳健性,Lowe建议对每个特征点使用4x4共16个种子点来描述,每个种子点有8个方向向量信息,这样每个特征点就有4x4x8共128个数据,即形成128维特征向量的特征描述符。此时,SIFT特征向量已除去了尺度变化、旋转等几何变形因素的影响,再继续将特征向量的长度归一化,则可以进一步去除光照变化的影响。
为了对光线变化更具鲁棒性,描述子都被归一化到单位长度。如果图像的对比度发生变化,每个像素值都会乘上一个数值,归一化后,对比度的影响被消除了。对于图像亮度的变化,每个像素值都会加上一个数值,然而这对计算的梯度是没有影响的。因此,该描述子对亮度的仿射变换是鲁棒的。对于非线性的光线变化,梯度大小会受影响,但是梯度的方向不会有大的变化,我们可以根据生物学原理解释此问题。在 128 维的单位向量中,滤除梯度大小大于 0.2的梯度值(即把大于0.2的都改为0.2),然后重新归一化。也就是说,梯度大小的作用被虚弱了,而方向信息的作用被强化了。0.2是实验得出的经验值。
特征匹配
以两个特征点描述符之间的欧式距离作为特征点匹配的相似度准则。假设特征点对p和q的特征描述符分别为Desp和Desq,则其欧式距离定义为:
首先采用优先k-d树进行优先搜索来查找每个特征点的两个近似最近邻特征点,如找出特征点p欧式距离最近和次近的两个邻居特征点q’和q’’,然后计算p与q’以及p与q’’两组描述符之间的欧式距离的比值r,如果r小于给定的阀值T,则视为匹配成功,接受点对(p,q’)为图像序列中的一对匹配点,否则匹配失败。
如图4.9所示,是特征点随最近邻域与次邻域距离比值的分布概率图,水平坐标表示最近邻域距离与次邻域距离的比值比;垂直坐标表示正确匹配的特征点(即“内点”,图中inliers曲线表示)和错误匹配的特征点(即"外点”,图中outliers曲线表示)。两条曲线相交于最近邻域距离与次邻域距离的比值为0.75,这说明小于0.75时,检测到的特征点为"内点"的概率比"外点"大,而且大很多。通常选择阀值为0.6.
具体可参考:http://blog.csdn.net/xiaowei_cqu/article/details/8069548