软考路之算法汇总

背景：软考准备的过程中总会出现比较棘手的问题，而算法设计部分就是一块儿比较“难啃的骨头”。软考后面的第四道大题就是算法分析题，考验我们的逻辑分析能力和算法分析能力，Are you ready？开始我们的算法旅程吧！

一、算法

    算法（Algorithm）是对待问题求解步骤的一种描述，它是指令的有限序列，其中每一条指令表示一个或多个操作。此外，一个算法还具有5个重要特征：有穷性、确定性、可行性、输入、输出。

二、算法分析

    通常，求解一个问题可能会有多种算法可以选择，选择的主要标准首先是算法的正确性、可靠性、简单性和易理解性。其次是算法的时间复杂度和空间复杂度要低。

    在计算机资源中，最重要的是时间和空间（存储器）资源，因此复杂度分析主要包括时间复杂度和空间复杂度。

三、算法的表示

    常用的表示算法的方法有自然语言、流程图、程序设计语言和伪代码。

四、算法设计

    递归是指子程序（或函数）直接调用自己或通过一系列调用语句间接调用自己。

    递归的两个基本要素：边界条件，即确定递归到何时终止，也称为递归出口；递归模式，即大问题是如何分解为小问题的，也称递归体。

    例：阶乘函数

    int Factorial（int num）{
        if(num == 0)
           return 1;
        if(num > 0)
           return num * Factorial(num - 1);
       }

1、分治法

    分治与递归时一对孪生兄弟。

    基本思想：将一个难以直接解决的大问题分解成一些规模较小的相同问题，以便各个击破，分而治之。

    一般来说分治算法在每一层递归上都有3个步骤：

   （1）分解。将原问题分解成一系列子问题。

   （2）求解。递归地求解各子问题。若子问题足够小，则直接求解。

   （3）合并。将子问题的杰合并成原问题的解。

    例1：归并排序

    （1）分解。将 n 个元素分成各含n/2个元素的子序列。

    （2）求解。用递归排序对两个子序列递归地排序。

    （3）合并。合并两个已经拍好序的子序列以得到排序结果。

    例2：最大字段和问题

2、动态规划法

    基本思想：将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。

    与分治法比较：经分解的子问题往往不是独立的。

    动态规划算法能找出其中的一个最优解，步骤为：

    （1）找出最优解的性质，并刻画其结构特征。

    （2）递归地定义最优解的值。

    （3）以自底向上的方式计算出最优值。

    （4）根据计算最优值时得到的信息，构造一个最优解。

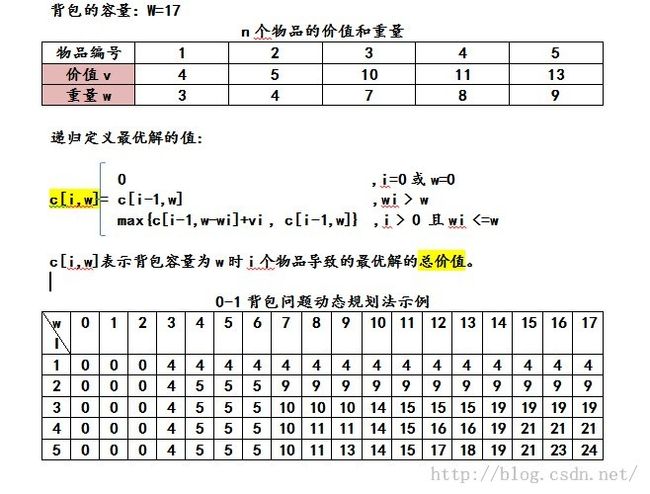
    例：0-1背包问题

由上表格可知最优的是24，所以其最优解为（0，0，0，1，1）

3、贪心法

    基本思想：贪心法并不是从整体最优考虑，它所做出的选择只是在某种意义上的局部最优。这种局部最优选择并不能保证总能获得全局最优解，但通常能得到较好的近似最优解。

    与动态规划法比较：贪心法在解决问题的策略上是仅根据当前已有的信息做出选择，而且一旦做了选择，不管将来有什么结果，这个选择都不会改变。

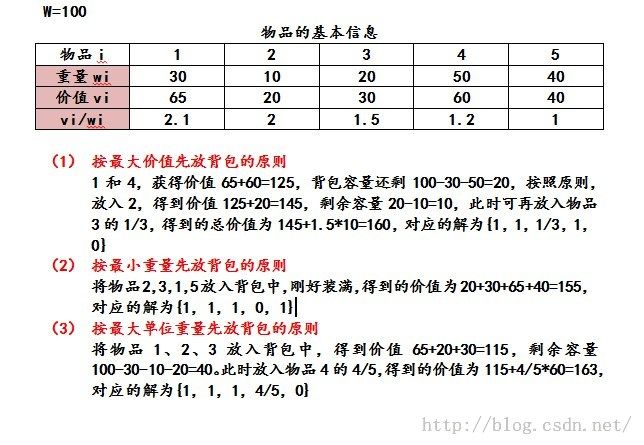
    例：背包问题

  

4、回溯法

    基本思想：在确定了解空间的组织结构后，回溯法从开始结点（根结点）出发，以深度优先的方式搜索整个解空间。

    开始结点就是一个活结点，同时也成为当前的扩展结点。在当前的扩展结点处，搜索向纵深方向移至一个新结点。这个新结点就成为一个新的活结点，并成为当前扩展结点。如果，在当前扩展结点处不能再向纵深方向移动，则当前的扩展结点就成为死结点。此时，应往回移动（回溯）至最近的一个活结点处，并使这个活结点成为当前的扩展结点。

    回溯法即以上述的工作方式递归地在解空间中搜索，直到找到所要求的解或解空间中已无活结点为止。

    步骤：

    （1）针对所给问题，定义问题的解空间。

    （2）确定易于搜索的解空间结构。

    （3）以深度优先的方式搜索解空间。

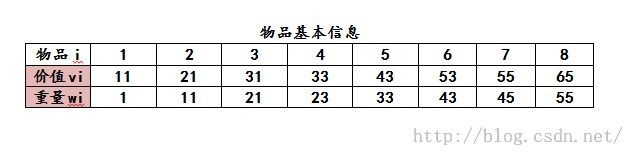
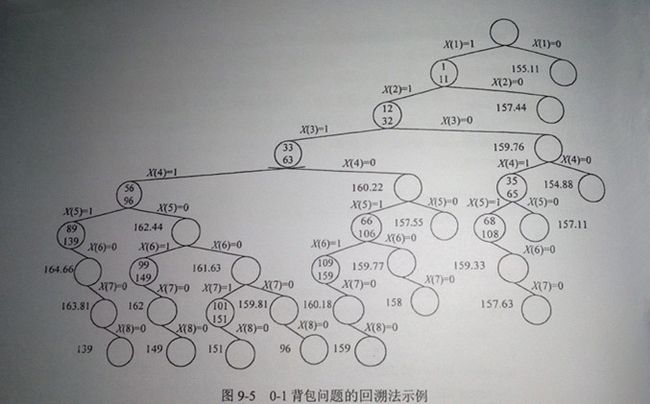
    例：

    如图可知有五个可行解（139，149.151，96，159），可知最优的为159，所以最优解为（1，1，1，0，1，1，0，0）

5、其他

分支限界法

    类似回溯法，也是一种在问题的空间树T上搜索问题解的算法。

    与回溯法比较：回溯法的求解目标是找出满足约束条件的所有解。而分支限界法的求解目标是找出满足约束条件的一个解，或是在满足约束调节的解中找出使某一目标函数达到极大或极小的解，即在某种意义下的最优解。

概率算法

    基本特征：（1）输入包括两部分：原问题的输入，供算法进行随机选择的随机数序列。

              （2）在运行过程中，包括一处或多出随机选择，根据随机值来决定算法的运行路径。

              （3）结果不能保证一定是正确的，但能限制其出错概率。

              （4）对于相同的输入实例，概率算法执行的时间可能不同。

    类型：数值概率算法、蒙特卡罗算法、拉斯维加斯算法、舍伍德算法

近似算法

    基本思想：放弃求最优解，而用近似最优解代替最优解，以换取算法设计上的简化和时间复杂度的降低。

    两个重要标准：算法的时间复杂度，解的近似程度

五、学习心得

    用批判性的目光看待事物。每种算法都有自己的优点的不足。

    适合自己的就是最好的。不同的问题是用的算法不同，但是最优的只用一个，找到适合某问题的就是最好的。