数据结构：关于重建二叉树的三种思路

前言：

  前几天在温习《编程之美》这本书的时候，看到了二叉树的重建。正好，也想复习一下数据结构的知识，就来写了一个小Demo。居然有新发现(本文中的第三种方式)。

  我们在学习数据结构的时候，肯定可以很轻松地编写对二叉树的三种遍历过程。分别是前序、中序和后序遍历。

  这里要说的不是对二叉树遍历，而是要通过一些遍历过程来重建一棵二叉树。比例，告诉你有一棵二叉树前序遍历的结果为：ABC；中序遍历的结果为：BAC。我们可以很轻松地写出这棵二叉树就是以A为根节点、其左孩子是B、右孩子是C。那么从代码的角度，或者说是从算法的角度又要怎么来编写程序呢？

本文链接：http://blog.csdn.net/lemon_tree12138/article/details/49798221 -- Coding-Naga
                                                                 --转载请注明出处

二叉树的遍历过程：

图-1 二叉树的前序遍历

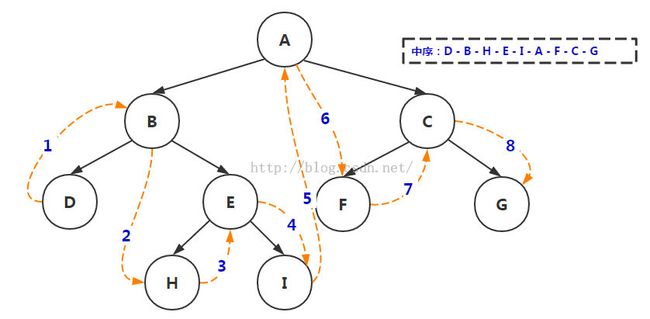
图-2 二叉树的中序遍历

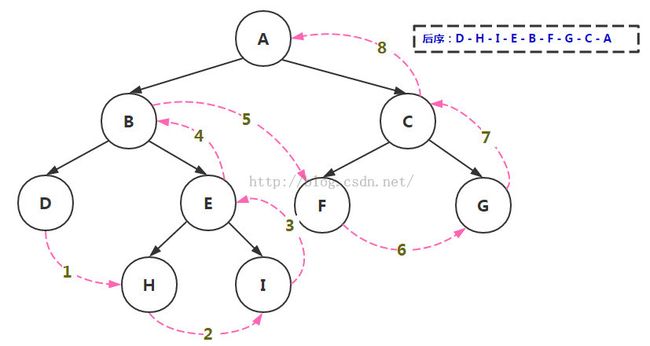
图-3 二叉树的后序遍历

思路说明：

这里我会采用三种不同的方法来说明其重建过程，代码部分则是采用其中一种来作详解。

而具体数据如下：

前序：A B D E H I C F G
中序：D B H E I A F C G

1.递归重建

  在上面的前序序列中，我们可以很容易地获得A就是根节点。此时，我们可以在后序序列中找到这个A，那么在A的左边就是A的左孩子及其子节点，在A的右边就是A的右孩子及其子节点。假设，我们目前在A的左边。在遍历前序序列到B的时候，我就知道了B就是A的左孩子，而在B的左边(中序序列)的都是B的左孩子及其子节点，在B的右边(同是也在A的左边)的就是B的右孩子及其子节点...以此类推.这就是利用递归来重建二叉树。

2.建立节点集

  关于这种方法，如果你对B树有所了解，也就不难理解了。因为后面我会单独写一篇关于B树的文章，这里就暂时一笔代过，说说思路就好了。

  为子节点建立节点集。在遍历(前/后序遍历的序列)的过程中，分裂和修正这个节点集。

3.创建索引函数

  前面的两种方法，其实可以说是同一种方法，也是比较常见的方法，《编程之美》里使用的正是常见的递归调用。下面的这种方法是本文的重点，我在其他地方并没有见到过类似的方法，于是在此记录一下思路和过程。我当时也只是灵光一闪，想到还可以用这样巧妙的方法来实现。真是让人兴奋。下面看看具体实现过程。

  让前/后序遍历的序列拥有中序遍历序列的索引，在遍历(前/后序遍历的序列)的过程中按照二叉排序树的方法直接插入即可.

图-4 节点索引函数对照表

  看到这个表，是不是有一种似曾相识的感觉。这个在KMP模式匹配也有一个类似的INDEX函数，在KMP里叫作next.这里我给他取名叫作index吧。因为这个index很直观，就是取了某一个节点的下标，并保存。

  其实在已知的遍历序列中，如果含有中序遍历结果，那么我们都可以采用上面的这种创建索引函数的方式来简化重建过程。可能你会问我为什么会这样？下面请看图-4.

图-5 二叉树的中序遍历顺序示意图

  我们可以把图-2中的中序遍历二叉树过程平摊开，就可以获得图-5中这样的一个顺序序列。

  从上面的图-5中我们可以发现一个现象，那就是某一个节点的左孩子一定是在这个节点的左边，其右孩子一定是在这个节点的右边(当然，这个现象也可以从中序遍历的定义获得)。也就是节点Node的左孩子Left的值一定是比Node的值小，而Node右孩子Right的值一定是比Node的值大。

  这样的一些描述是不是似曾相识呢？没错，在二叉排序树中正是这样定义的。

  现在，我们再来看看二叉树的前序遍历过程。因为是前序，所以我们在遍历节点Node的孩子节点之前，必定是已经遍历过Node的孩子节点。这样也可以理解成是一种临近遍历的过程。

  这样看来，前序 + 中序 = 二叉排序树。于是，我们就有了以下代码：

节点(Node)：

public class Node {

    String name;
    Node leftNode;
    Node rightNode;
    int index;

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public Node getLeftNode() {
        return leftNode;
    }

    public void setLeftNode(Node leftNode) {
        this.leftNode = leftNode;
    }

    public Node getRightNode() {
        return rightNode;
    }

    public void setRightNode(Node rightNode) {
        this.rightNode = rightNode;
    }

    public int getIndex() {
        return index;
    }

    public void setIndex(int index) {
        this.index = index;
    }
}

主函数(RestoreBinTree)：

public class RestoreBinTree {

    Node root = null;

    public static void main(String[] args) {
        RestoreBinTree m = new RestoreBinTree();
        String[] F = {"A", "B", "D", "E", "H", "I", "C", "F", "G"};
        String[] L = {"D", "B", "H", "E", "I", "A", "F", "C", "G"};
        m.restoreTree(F, L);
        System.out.println(m.root);
    }

    /**
     * 重建二叉树
     * @param labelFirst
     * @param labelLast
     */
    public void restoreTree(String[] labelFirst, String[] labelLast) {
        int[] r = recordArray(labelFirst, labelLast);

        if (root == null) {
            root = new Node();
            root.setName(labelFirst[0]);
            root.setIndex(r[0]);
        }

        for (int i = 1; i < labelFirst.length; i++) {
            Node currentNode = new Node();
            currentNode.setName(labelFirst[i]);
            currentNode.setIndex(r[i]);

            insert(currentNode);
        }
    }

    /**
     * 向二叉树中插入一个节点
     * @param insertNode
     */
    public void insert(Node insertNode) {
        Node currentNode = root;
        while (true) {
            if (insertNode.getIndex() < currentNode.getIndex()) {
                if (currentNode.getLeftNode() == null) {
                    currentNode.setLeftNode(insertNode);
                    break;
                } else {
                    currentNode = currentNode.getLeftNode();
                }
            } else if (insertNode.getIndex() > currentNode.getIndex()) {
                if (currentNode.getRightNode() == null) {
                    currentNode.setRightNode(insertNode);
                    break;
                } else {
                    currentNode = currentNode.getRightNode();
                }
            } else {
                break;
            }
        }
    }

    /**
     * 计算索引函数
     * @param labelFirst
     * @param labelLast
     * @return
     */
    public int[] recordArray(String[] labelFirst, String[] labelLast) {
        if (labelFirst == null || labelFirst.length == 0 || labelLast == null || labelLast.length == 0) {
            return null;
        }

        int[] record = new int[labelFirst.length];
        for (int i = 0; i < labelFirst.length; i++) {
            record[i] = index(labelLast, labelFirst[i]);
        }

        return record;
    }

    /**
     * 计算索引函数
     * @param labels
     * @param label
     * @return
     */
    private int index(String[] labels, String label) {
        for (int i = 0; i < labels.length; i++) {
            if (label.equals(labels[i])) {
                return i;
            }
        }

        return -1;
    }
}

REF:

《编程之美》