【CareerCup】Trees and Graphs—Q4.2
转载请注明出处:http://blog.csdn.net/ns_code/article/details/23206519
题目:
Given a directed graph, design an algorithm to find out whether there is a route between two nodes.
翻译:
给定一个有向图,设计算法判断两结点间是否存在路径。
思路:
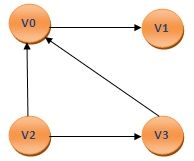
考察图的遍历,如果遍历路径上经过该顶点,则存在路径,不经过则不存在路径,在遍历算法上做一些改进即可。我们这里用图的DFS来改进。并采用图的BFS和DFS一文中的有向图来作测试,并采用邻接矩阵来存储该有向图中的边和顶点信息。
实现代码:
/*
DFS遍历保存路过的顶点字符
*/
int count = 0;
char BL[NUM]; //用来保存遍历路过的顶点字符
void DFS(Graph Gp, int begin)
{
BL[count++] = Gp[begin].data;
visited[begin] = true;
//循环访问当前节点的所有邻接点(即该节点对应的链表)
int i;
for(i=first_vertex(Gp,begin); i>=0; i=next_vertex(Gp,begin,i))
{
if(!visited[i]) //对于尚未遍历的邻接节点,递归调用DFS
DFS(Gp,i);
}
}
/*
判断两个顶点是否连通
*/
bool isArrived(Graph Gp,int begin,int end)
{
DFS(Gp,begin);
int i;
for(i=0;i<count;i++)
if(BL[i] == Gp[end].data)
return true;
return false;
}
完整代码:
/**********************************
题目描述:
给定一个有向图,设计算法判断两结点间是否存在路径
Date:2014-04-08
**********************************/
#define NUM 4 //图中顶点的个数
bool visited[NUM]; //定义全局变量辅助数组,用来保存每个节点的访问信息
/*
用邻接表作为图的存储结构
在邻接表中,用一个一维数组存储图中的每个顶点的信息,
同时为每个顶点建立一个单链表,链表中的节点保存依附在该顶点上的边或弧的信息
*/
typedef struct node
{ //链表中的每个节点,保存依附在该节点上的边或弧的信息
int vertex; //在有向图中表示该弧所指向的顶点(即弧头)的位置,
//在无向图中表示依附在该边上的另一个顶点的位置
struct node *pNext; //指向下一条依附在该顶点上的弧或边
}Node;
typedef struct head
{ //数组中的每个元素,保存图中每个顶点的相关信息
char data; //顶点的数据域
Node *first; //在有向图中,指向以该顶点为弧尾的第一条弧
//在无向图中,指向依附在该顶点上的第一条边
}Head,*Graph; //动态分配数组保存每个顶点的相关信息
//根据图例创建对应的图
Graph create_graph();
//返回图中指定序号顶点的第一个邻接点
int first_vertex(Graph,int);
//返回图中指定序号节点的下一个邻接点
int next_vertex(Graph,int,int);
//DFS保存路过的顶点字符
void DFS(Graph, int);
//判断两顶点是否连通
bool isArrived(Graph,int,int);
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int main()
{
Graph Gp = create_graph();
memset(visited,0,sizeof(visited));
if(isArrived(Gp,3,2))
printf("D To C Existed\n");
else
printf("D To C Not Existed\n");
if(isArrived(Gp,1,2))
printf("B To C Existed\n");
else
printf("B To C Not Existed\n");
if(isArrived(Gp,3,1))
printf("D To B Existed\n");
else
printf("D To B Not Existed\n");
if(isArrived(Gp,0,3))
printf("A To D Existed\n");
else
printf("A To D Not Existed\n");
int i;
//释放掉为每个单链表所分配的内存
for(i=0;i<NUM;i++)
{
free(Gp[i].first);
Gp[i].first = 0; //防止悬垂指针的产生
}
//释放掉为顶点数组所分配的内存
free(Gp);
Gp = 0;
return 0;
}
/*
根据图例创建对应的图
*/
Graph create_graph()
{
//为保存顶点相关信息的数组分配空间,并对数据域赋值
Graph graph = (Graph)malloc(NUM*sizeof(Head));
int i;
//顶点的序号按照输入顺序从0依次向后
for(i=0;i<NUM;i++)
graph[i].data = 'A' + i;
//为每个节点对应的的单链表中的节点分配空间
Node *p00 = (Node *)malloc(sizeof(Node));
Node *p20 = (Node *)malloc(sizeof(Node));
Node *p21 = (Node *)malloc(sizeof(Node));
Node *p30 = (Node *)malloc(sizeof(Node));
//为各单链表中的节点的相关属性赋值
p00->vertex = 1;
p00->pNext = NULL;
p20->vertex = 0;
p20->pNext = p21;
p21->vertex = 3;
p21->pNext = NULL;
p30->vertex = 0;
p30->pNext = NULL;
//将顶点与每个单链表连接起来
graph[0].first = p00;
graph[1].first = NULL;
graph[2].first = p20;
graph[3].first = p30;
return graph;
}
/*
返回图Gp中pos顶点(序号为pos的顶点)的第一个邻接顶点的序号,如果不存在,则返回-1
*/
int first_vertex(Graph Gp,int pos)
{
if(Gp[pos].first) //如果存在邻接顶点,返回第一个邻接顶点的序号
return Gp[pos].first->vertex;
else //如果不存在,则返回-1
return -1;
}
/*
cur顶点是pos顶点(cur和pos均为顶点的序号)的其中一个邻接顶点,
返回图Gp中,pos顶点的(相对于cur顶点)下一个邻接顶点的序号,如果不存在,则返回-1
*/
int next_vertex(Graph Gp,int pos,int cur)
{
Node *p = Gp[pos].first; //p初始指向顶点的第一个邻接点
//循环pos节点对应的链表,直到p指向序号为cur的邻接点
while(p->vertex != cur)
p = p->pNext;
//返回下一个节点的序号
if(p->pNext)
return p->pNext->vertex;
else
return -1;
}
/*
DFS遍历保存路过的顶点字符
*/
int count = 0;
char BL[NUM]; //用来保存遍历路过的顶点字符
void DFS(Graph Gp, int begin)
{
BL[count++] = Gp[begin].data;
visited[begin] = true;
//循环访问当前节点的所有邻接点(即该节点对应的链表)
int i;
for(i=first_vertex(Gp,begin); i>=0; i=next_vertex(Gp,begin,i))
{
if(!visited[i]) //对于尚未遍历的邻接节点,递归调用DFS
DFS(Gp,i);
}
}
/*
判断两个顶点是否连通
*/
bool isArrived(Graph Gp,int begin,int end)
{
DFS(Gp,begin);
int i;
for(i=0;i<count;i++)
if(BL[i] == Gp[end].data)
return true;
return false;
}
测试结果:
注:代码开源到Github:https://github.com/mmc-maodun/CareerCup