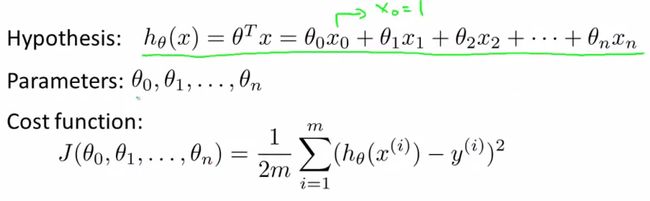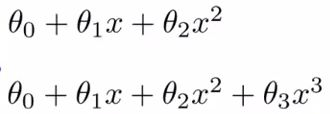Machine Learning课程笔记2——线性回归2
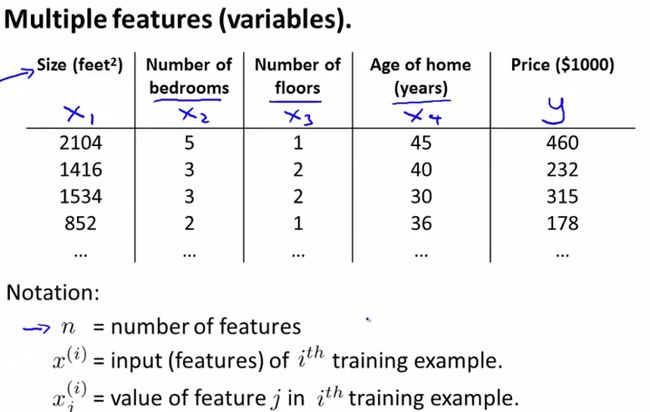
2、多变量的线性回归(一般化)
因为前面在单变量的部分已经说得比较详细了,这里就简要一些吧。
梯度下降算法的运用:
特征缩放:
为了使得梯度下降得更快,梯度下降所需要的循环次数减少,我们需要对训练集的数据进行特征缩放,使得特征值都具有相近的size
最简单的方法就是x=(x-ave_value)/rangesize (减平均值后除以标准差 ) 通常使得x在 -1~1 范围比较合适,这个数据不是严格限制的,如-3~3或者-0.5~0.5 也可以。
在等高线图上能很直观的看到,如果房子的面积为0-2000平方英尺,而房间数量为0-5的话图形会很扁,收敛时间很长,通过特征缩放可以使得图形更圆,收敛加快。
学习率:
前面说过学习率太大或太小都不合适,
不同模型所对应的梯度下降的迭代次数不同,我们可以根据代价函数的变化值小于0.001来表明已经收敛,如下图的显示更直观,在迭代次在300到400之间时已经接近平坦,那么就认为已经收敛。
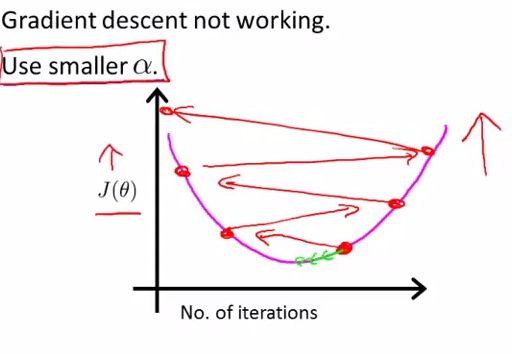
如果学习率太小,那么迭代次数会很大,收敛会很慢;而如果你发现代价函数不是在变小而是在变大,或者有时变小有时变大等,很可能是你的学习率选取得太大,如下图:
选择学习率时,可以...0.001, 0.003, 0.01, 0.03, 0.1, 0.3 ,1, ....
多项式回归:
通常直线并不能很好的拟合,所以我们需要曲线来适应我们的数据,如
通常我们需要先观察数据然后决定尝试什么样的模型。而且在特征值的选择上我们也可以进行优化,如房子的长和宽两个特征量可以用面积这一个特征量来表示。
正规方程组:
h=theta ' * X;
octave: theta = pinv(X'*X)*X'*y;