hdu 3340 Rain in ACStar(成段更新)
题意:有T组测试数据,每组数据有N个操作,(1)“R P”,表示掉下了一个P边形,接下来的一行里,给出这P个点的坐标——首先是最左边的点,然后从这点开始逆时针给出其他点。(2)"Q A B“,查询数轴上区间[A,B]内面积的和。
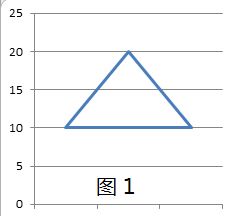
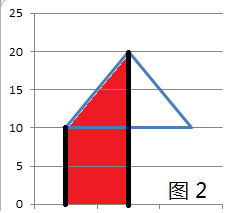
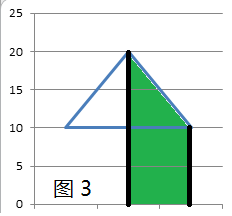
易知,图1里的那个三角形的面积是通过,图2里红色的面积加上图3里绿色的面积,然后减去图4里黄色的面积。
这些图形都可以转化成梯形,即在一段区间[A,B]里,A加上首项为add1,B加上末项为add2,长度为B-A+1,公差是(add2-add1)/(B-A+1)的等差数列。
我们从最左边的那一点开始遍历,如果当前点的x坐标小于它的下一点的x坐标,那么就减去由当前点、下一点以及数轴构成的梯形的面积,反之则加上。那么问题就是延迟标记是什么,如何传递。这就和 Uva 12436 Rip Van Winkle's Code这道题很类似(解题报告Here)。等差数列叠加了,还是等差数列,性质没有改变。所以在线段树的结点里,记录左端点要加多少add1,右端点要加多少add2,以及公差step。向下传递的时候,将区间分解成两部分,区间中点要加多少,可以通过等差数列的分工计算出来。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <map>
#include <algorithm>
using namespace std;
#define LL(x) (x<<1)
#define RR(x) (x<<1|1)
#define MID(a,b) (a+((b-a)>>1))
const int N=125010;
struct node
{
int lft,rht,len;
double add1,add2,step,sum;
int mid(){return MID(lft,rht);}
void init() { add1=add2=step=sum=0; }
void fun(double a,double b,double c)
{
add1+=a; add2+=b; step+=c;
sum+=(a+b)*len/2;
}
};
vector<int> sca;
map<int,int> H;
struct OP
{
int type,n;
int x[6],y[6];
void get()
{
char str[5];
scanf("%s",str);
if(str[0]=='R')
{
type=0;
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d%d",&x[i],&y[i]);
sca.push_back(x[i]);
}
}
else
{
type=1;
scanf("%d%d",&x[0],&y[0]);
sca.push_back(x[0]);
sca.push_back(y[0]);
}
}
}op[N/5];
struct Segtree
{
node tree[N*4];
double calu(int st,int ed,double add1,double step)
{
int len=sca[ed]-sca[st];
return add1+len*step;
}
void PushUp(int ind)
{
tree[ind].sum=tree[LL(ind)].sum+tree[RR(ind)].sum;
}
void PushDown(int ind)
{
double add1=tree[ind].add1,add2=tree[ind].add2,step=tree[ind].step;
double tmp=calu(tree[ind].lft,tree[ind].mid(),add1,step);
tree[LL(ind)].fun(add1,tmp,step);
tree[RR(ind)].fun(tmp,add2,step);
tree[ind].add1=tree[ind].add2=tree[ind].step=0;
}
void build(int lft,int rht,int ind)
{
tree[ind].lft=lft; tree[ind].rht=rht;
tree[ind].init(); tree[ind].len=sca[rht]-sca[lft];
if(lft+1!=rht)
{
int mid=tree[ind].mid();
build(lft,mid,LL(ind));
build(mid,rht,RR(ind));
}
}
void updata(int st,int ed,int ind,double add1,double add2,double step)
{
int lft=tree[ind].lft,rht=tree[ind].rht;
if(st<=lft&&rht<=ed) tree[ind].fun(add1,add2,step);
else
{
PushDown(ind);
int mid=tree[ind].mid();
if(ed<=mid) updata(st,ed,LL(ind),add1,add2,step);
else if(st>=mid) updata(st,ed,RR(ind),add1,add2,step);
else
{
double tmp=calu(st,mid,add1,step);
updata(st,mid,LL(ind),add1,tmp,step);
updata(mid,ed,RR(ind),tmp,add2,step);
}
PushUp(ind);
}
}
double query(int st,int ed,int ind)
{
int lft=tree[ind].lft,rht=tree[ind].rht;
if(st<=lft&&rht<=ed) return tree[ind].sum;
else
{
PushDown(ind);
int mid=tree[ind].mid();
double sum=0;
if(st<mid) sum+=query(st,ed,LL(ind));
if(ed>mid) sum+=query(st,ed,RR(ind));
PushUp(ind);
return sum;
}
}
}seg;
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
sca.clear(); H.clear();
int n;
scanf("%d",&n);
for(int i=0;i<n;i++) op[i].get();
sort(sca.begin(),sca.end());
sca.erase(unique(sca.begin(),sca.end()),sca.end());
for(int i=0;i<(int)sca.size();i++) H[sca[i]]=i;
seg.build(0,(int)sca.size()-1,1);
for(int i=0;i<n;i++)
{
int x1,y1,x2,y2;
if(op[i].type==0)
{
for(int j=0;j<op[i].n;j++)
{
x1=op[i].x[j]; y1=op[i].y[j];
x2=op[i].x[(j+1)%op[i].n]; y2=op[i].y[(j+1)%op[i].n];
if(x1>x2) swap(x1,x2),swap(y1,y2);
else y1=-y1,y2=-y2;
double step=(y1*1.-y2*1.)/(x1*1.-x2*1.);
seg.updata(H[x1],H[x2],1,y1,y2,step);
}
}
else
{
x1=op[i].x[0],y1=op[i].y[0];
printf("%.3lf\n",seg.query(H[x1],H[y1],1));
}
}
}
return 0;
}