hdu 4533 威威猫系列故事——晒被子（成段更新）

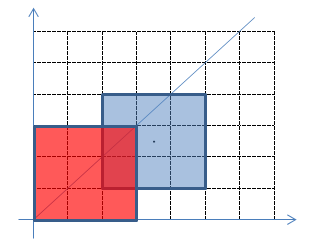
题意：给你N个矩形，每个矩形给出左下角坐标，右上角坐标，有M个询问，每个询问给出一个时间t，问(0,0)，(t,t)的范围内矩形的面积和（重叠的也算）。

用树状数组去维护A*t*t+B*t+C这个式子的A,B,C三个系数，维护在不同的t时，ABC分别应该为多少。

分成三个阶段。

在这个阶段，计算面积的公式为(t-x1)*(t-y1)，因式分解之后，得到三个系数的值。这种情况是max(x1,y1)<min(x2,y2)，所以更新的区间是[ max(x1,y1),min(x2,y2) ]。

在这个阶段，计算的公式为(t-x1)*(t-y1)-(t-x1)*(t-y2)，同样因式分解之后，得到三个系统的值。这种情况更新的区间要小心，应该是[ max(x1,y2)+1, x2 ]。另外一种矩阵情况也是一样的，不再赘述。

最后，面积就应为(x2-x1)*(y2-y1)。更新的范围就是max(x2,y2)+1。

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N=200005;
typedef long long LL;
struct BIT
{
    LL T[N];
    int lowbit(int x) {return x&(-x);}
    void clear(){memset(T,0,sizeof(T));}
    void add(int st,int ed,LL valu)
    {
        for(int i=st;i<N;i+=lowbit(i)) T[i]+=valu;
        for(int i=ed+1;i<N;i+=lowbit(i)) T[i]-=valu;
    }
    LL query(int pos)
    {
        LL sum=0;
        for(int i=pos;i>0;i-=lowbit(i)) sum+=T[i];
        return sum;
    }
}A,B,C;
void fun(int st,int ed,LL a,LL b,LL c)
{
    A.add(st,ed,a);
    B.add(st,ed,b);
    C.add(st,ed,c);
}
int main()
{

    int t;
    scanf("%d",&t);
    while(t--)
    {
        A.clear(); B.clear(); C.clear();

        int n,m;
        scanf("%d",&n);

        for(int i=0;i<n;i++)
        {
            LL x1,y1,x2,y2;
            scanf("%I64d%I64d%I64d%I64d",&x1,&y1,&x2,&y2);

            if(max(x1,y1)<min(x2,y2))
                fun(max(x1,y1),min(x2,y2),1,-(x1+y1),x1*y1);

            if(x2<y2) fun(max(x2,y1)+1,y2,0,-x1+x2,y1*(x1-x2));
            if(y2<x2) fun(max(y2,x1)+1,x2,0,-y1+y2,x1*(y1-y2));

            fun(max(x2,y2)+1,N,0,0,(x2-x1)*(y2-y1));
        }

        scanf("%d",&m);
        while(m--)
        {
            LL t;
            scanf("%I64d",&t);


            LL ans=0;
            ans+=A.query(t)*t*t;
            ans+=B.query(t)*t;
            ans+=C.query(t);

            printf("%I64d\n",ans);
        }
    }
    return 0;
}