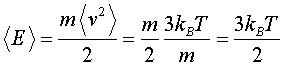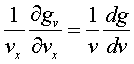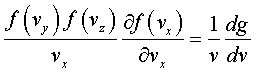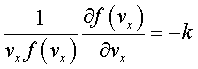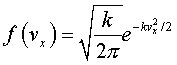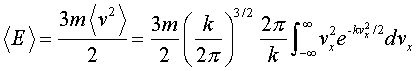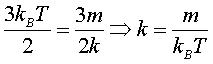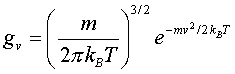Maxwell-Boltzmann分布函数的推导
Maxwell-Boltzmann几率分布函数可用于确定气体分子的运动速率。因为我们要处理大量气体分子，所以需要应用统计方法得到一个气体分子速率的统计表达式。我们的模型是：在一个立方容器中有一个由单一气体分子组成的气体体系，假定气体符合理想气体状态方程，气体分子可近似看作刚性球体，分子之间不存在分子间相互作用力。
首先，我们写出气体分子撞击器壁器壁的次数N的表达式：
(1)
在上式中，我们只写出了气体速度在x轴方向上的分量。其中，rN为气体分子的密度（气体分子个数/单位体积），A为器壁的面积，Dt为气体分子的飞行时间，f(vx)为速率分布函数。上式中加和符号是指把所有vx>0(分子向x轴正向运动)的分子考虑在内。
气体分子撞击器壁所引起的器壁动量改变量为：
(2)
所以，器壁所受压力为：
(3)
由于我们假定气体处于稳态，所以全部正速度气体分子速率之和等于全体气体分子速率之和的一半。
(4)
这时，我们把微观粒子的速率与气体的宏观性质联系起来。引入理想气体状态方程，于是得到：
(5)
上式右侧的加和可以用统计符号<vx2>表达为：
(6)
上式括号中为分子的均方根速率。下面用分子数目N与气体体积V之比来取代密度rN：
(7)
消去两边的V，得到
(8)
分子的数目可以用气体的摩尔量和Avogadro常数的乘积取代，
(9)
消去两边共有的摩尔量n，同时合并分子质量和Avogadro常数，得：
(10)
上式给出了理想气体分子速率与温度和分子量的关系。此时，它是分子沿x轴方向的均方根速率。因为我们的体系是三维体系，所以要把上式推广到三维。因为我们假定气体处于稳态（各向同性），因此有：
(11)
因此，最终我们得到:
(12)
从上式中，我们也可以引入一个新的常数，得到气体的平均动能，
(13)
式(13)的kB为Boltzmann常数，它的近似值为1.38´10-23J/K。
把上述两个式子代入到方程(12)中，得：
(14)
因此，经典物理的动能为：
(15)
上式表明，理想气体的平均动能仅仅依赖它的温度。
现在可以方便地导出一个与气体的某些状态参数相关的函数，用来描述气体分子的速率分布。对于理想气体，这是很容易的。设有一个分布函数，它等于三个坐标轴方向分量的乘积。
(16)
求g相对于坐标变量vx的导数，然后使用链率(chain rule):
(17)
\ 
(18)
上式两边同除以vx，得：
(19)
然后把g的表达式(方程(16))代入，得：
(20)
求导后得到：
(21)
同理，我们可以得到与方程(17)相似的另外两个方程：
(22)
和
(23)
同时从方程(21)、(22)和(23)除以g，得到
(24)
为了保证这个方程的三个等号同时成立，上面方程必须对所有的vx、vy、vz值都有解。由于各式具有完全独立的变量，因此方程的左侧必然是一个常数。这里为方便起见，我们使用-k。
(25)
这个一阶微分方程很容易求解。整理一下上式，得：
(26)
对上式两边积分，得：
(27)
其中，N为积分常数。为确定N的数值，我们认识到对于任何几率分布，上述积分必定是归一化的。即，
(28)
这个积分可以从积分表中查到，于是得到：
(29)
重排得：
(30)
所以，函数f为：
(31)
下面将确定k值。返回到g的定义：
(32)
将方程(31)代入，得：
(33)
为确定k值，我们把g代入方程(15)，得到：
(34)
简化后得：
(35)
查积分表，得：
(36)
约化得：
(37)
将此式代入方程(15)，得：
(38)
于是我们得到x方向的Maxwell-Boltzmann分布函数：
(39)
将式(38)代回到式(32)，得到直角坐标系下的Maxwell-Boltzmann分布函数：
(40)
我们把式(16)的直角坐标系转换为球极坐标系，得到：
(41)
把式(40)代入到式(41)，得到球极坐标下的Maxwell-Boltzmann分布函数：
(42)