算法设计与分析--霍夫曼树编码(C++实现)
问题描述:
设需要编码的字符集为{d1, d2, …, dn},它们出现的频率为{w1, w2, …, wn},应用哈夫曼树构造最短的不等长编码方案。
Huffman算法:
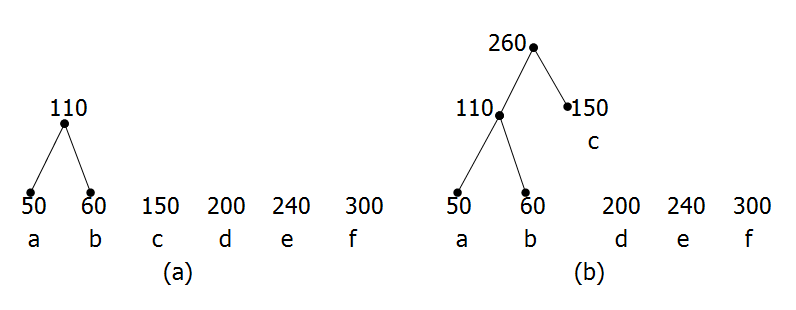
给定实数w1,w2,···,wt且 w1<=w2<=···<=wt
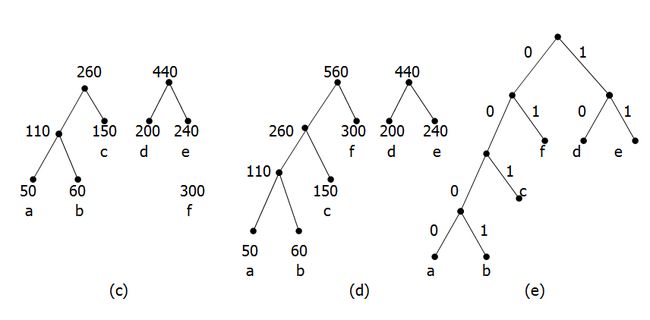
(1)连接w1,w2为权的两片树叶,得一分支点,其权为w1+w2 ;
(2)在w1+w2, w3+···+wt中选出两个最小的权,连接它们对应的顶点(不一定都是树叶),得分支点及所带的权;
(3)重复(2),直到形成t – 1个分支点,t片树叶为止。
算法实例:
C++代码:
#include<iostream>
#include<string>
using namespace std;
//结点类型
struct element
{
double weight; //字符出现的概率为实数
char ch;
int lchild, rchild, parent;
};
//在HuffTer中找权值最小的两个结点i1和i2
void Select(element huffTree[], int *a, int *b, int n)
{
int i;
double weight = 0;
for(i = 0; i <n; i++)
{
if(huffTree[i].parent != - 1) //如果有父结点的,不进行判断
continue;
else
{
if(weight == 0)
{
weight = huffTree[i].weight;
*a = i;
}
else
{
if(huffTree[i].weight < weight)
{
weight = huffTree[i].weight;
*a = i;
}
}
}
}
weight = 0;
for(i = 0; i < n; i++)
{
if(huffTree[i].parent != -1 || (i == *a))
continue;
else
{
if(weight == 0)
{
weight = huffTree[i].weight;
*b = i;
}
else
{
if(huffTree[i].weight < weight)
{
weight = huffTree[i].weight;
*b = i;
}
}
}
}
int temp;
if(huffTree[*a].lchild < huffTree[*b].lchild) //避免根结点的左右子树混淆
{
temp = *a;
*a = *b;
*b = temp;
}
}
//建立霍夫曼树
void HuffmanTree(element huffTree[], int w[], char ch[], int n)
{
for(int i = 0; i < 2 * n - 1;i++) //霍夫曼树共有2*n - 1个结点
{
huffTree[i].parent = -1; //双亲结点
huffTree[i].lchild = -1; //左孩子结点
huffTree[i].rchild = -1; //右孩子结点
}
for(int i = 0; i < n; i++) //构造n棵只含有根结点的二叉树
{
huffTree[i].weight = w[i]; //给哈夫曼树赋权值
huffTree[i].ch = ch[i]; //需要编码的字符
}
for(int k = n; k < 2 * n - 1; k++)//n-1次合并
{
int i1 = 0;
int i2 = 0;
Select(huffTree,&i1,&i2,k); //在HuffTer中找权值最小的两个结点i1和i2
huffTree[i1].parent = k; //将i1和i2合并,则i1和i2的双亲是k
huffTree[i2].parent = k;
huffTree[k].weight = huffTree[i1].weight + huffTree[i2].weight;
huffTree[k].lchild = i1;
huffTree[k].rchild = i2;
}
}
//霍夫曼编码
void HuffmanCode(element huffTree[], int n)
{
int i, j,k;
string s = "";
for(i = 0; i < n; i++) //在数组HuffTree中前n个元素是叶子结点,需要编码
{
s = ""; //编码s初始化为空串
j = i; //暂存i,不破坏循环变量
while(huffTree[j].parent != -1) //结点j存在双亲
{
k = huffTree[j].parent;
if(j == huffTree[k].lchild) //结点j是其双亲的左孩子
{
s = s + "0";
}
else //结点j是其双亲的右孩子
{
s = s + "1";
}
j = huffTree[j].parent; //将结点j的双亲赋给j
}
cout<<"字符"<<huffTree[i].ch<<"的编码:"<<endl;
for(int i =s.size() - 1; i >= 0; i--) //将s作为结点i的编码逆序输出
{
cout<<s.at(i)<<" ";
}
cout<<endl;
}
}
int main()
{
const int n = 6;
element huffTree[2 * n];
char ch[] = {'a', 'b', 'c','d','e','f'};
int w[] = {50, 60, 150, 200, 240, 300};
// 构造霍夫曼树
HuffmanTree(huffTree,w,ch,n);
//编码
HuffmanCode(huffTree,n);
system("pause");
return 0;
}
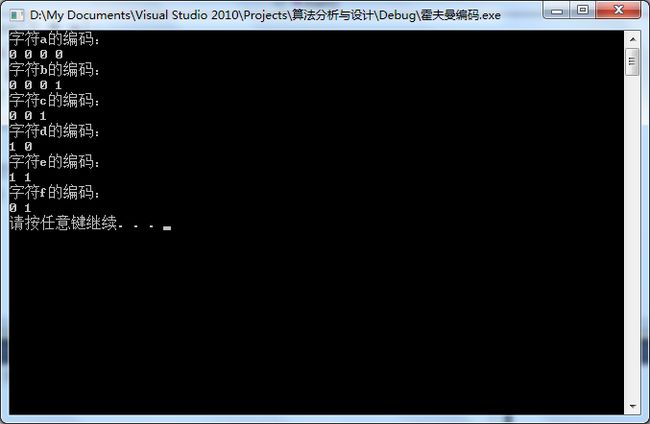
实验结果: