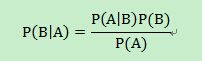Nani_xiao的机器学习与总结:Andrew Ng.机器学习(一) :贝叶斯定理
已知某条件概率,如何得到两个事件交换后的概率,也就是在已知P(A|B)的情况下如何求得P(B|A)。
P(A|B)表示事件B已发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式: ,
而贝叶斯定理为:
朴素贝叶斯基本思想:对于给出的待分类项,求解在此项条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。
分类算法之贝叶斯网络(Bayesiannetworks)
1、贝叶斯网络的解释和举例
朴素贝叶斯分类有一个限制条件,就是特征属性必须有条件独立或基本独立(实际上在现实应用中几乎不可能做到完全独立)。当这个条件成立时,朴素贝叶斯分类法的准确率是最高的,但不幸的是,现实中各个特征属性间往往并不条件独立,而是具有较强的相关性,这样就限制了朴素贝叶斯分类的能力。这一篇文章中,我们接着上一篇文章的例子,讨论贝叶斯分类中更高级、应用范围更广的一种算法——贝叶斯网络(又称贝叶斯信念网络或信念网络)。
EX1: 通过对训练数据集的统计,得到下表(R表示账号真实性,H表示头像真实性):
| R=0 |
R=1 |
| 0.11 |
0.89 |
|
|
H=0 |
H=1 |
| R=0 |
0.9 |
0.1 |
| R=1 |
0.2 |
0.8 |
纵向表头表示条件变量,横向表头表示随机变量。上表为真实账号和非真实账号的概率,而下表为头像真实性对于账号真实性的概率。这两张表分别为“账号是否真实”和“头像是否真实”的条件概率表。有了这些数据,不但能顺向推断,还能通过贝叶斯定理进行逆向推断。例如,现随机抽取一个账户,已知其头像为假,求其账号也为假的概率:

也就是说,在仅知道头像为假的情况下,有大约35.7%的概率此账户也为假。如果觉得阅读上述推导有困难,请复习概率论中的条件概率、贝叶斯定理及全概率公式。如果给出所有节点的条件概率表,则可以在观察值不完备的情况下对任意随机变量进行统计推断。上述方法就是使用了贝叶斯网络。
2、贝叶斯网络的定义及性质
一个贝叶斯网络定义包括一个有向无环图(DAG)和一个条件概率表组成。DAG中每一个节点表示一个随机变量,可以是直观观测变量或隐藏变量,而有向边表示随机变量间的条件依赖;条件概率表中的每一个元素对应DAG中唯一的节点,存储此节点对于其所有直接前驱节点的联合条件概率。
每一个节点在其直接前驱节点的值制定后,这个节点条件独立于其所有非直接前驱前辈节点。
贝叶斯网络可以看做是马尔科夫链(Markov)的非线性扩展。
一般情况下,多变量非独立联合条件概率分布有如下求取公式:

而在贝叶斯网络中,由于存在前述性质,任意随机变量组合的联合条件概率分布被化简成

其中Parents表示xi的直接前驱节点的联合,概率值可以从相应条件概率表中查到。
3、贝叶斯网络的构造和学习
构造和训练贝叶斯网络需要两步:
1) 确定随机变量间的拓扑关系,形成DAG。这一步通常需要领域专家完成,而想要建立一个好的拓扑结构,通常需要不断迭代和改进才可以。
2) 训练贝叶斯网络。需要完成条件概率表的构造,如果每个随机变量的值都是可以直接观察的,像上面的例子,这么这一步训练时直观的,方法类似于朴素贝叶斯分类。但是通常贝叶斯网络中存在隐藏变量节点,那么训练方法就比较复杂,例如梯度下降法。
4、贝叶斯网络的应用及示例
贝叶斯网络主要用于概率推理及决策,也就是在信息不完备的情况下通过可观察随机变量推断不可观察的随机变量,并且不可观察随机变量可以多余一个,一般初期将不可观察变量置为随机值,然后进行概率推理。
使用贝叶斯网络进行推理的步骤一般为:
1) 对所有可观察随机变量节点用观察值实例化,对不可观察节点实例化为随机值。
,其中wi表示除y以外的其他所有节点,a为正规化因子,sj表示y的第j个子节点。
3) 使用第二步计算出的各个y作为未知节点的新值进行实例化,重复第二步,知道结果充分收敛。
4) 将收敛结果作为推断值。