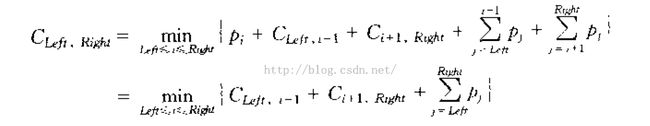《数据结构与算法分析》动态规划--矩阵乘法最优顺序、最优二叉查找树详解
前言:
最近感觉时间越来越紧张了,一堆的事情等着做,一堆的书等着看,真希望一天能有30个小时。
过了一周,这本书还是停留在第十章,这一章出现的算法太多,一个个实现确实花了不少的时间。
我的github:
我实现的代码全部贴在我的github中,欢迎大家去参观。
https://github.com/YinWenAtBIT
介绍:
一、动态规划:
定义:
当递归算法得到的程序时低效的时候,把递归算法改写为非递归算法能得到显著的性能提升,递归算法过程中使用的子问题的答案,会被记录在一个表内。这种方法就叫做动态规划。
二、动态规划的应用:
1. 斐波那契数列计算
2. 递归关系求解
3. 矩阵乘法顺序安排
4. 最优查找二叉树
这几个算法都是使用递归的话,会导致计算量按指数上升,同一个问题会被计算多次,所以改为非递归算法将显著提升其效率。三、斐波那契数列计算:
这个问题基本上是最简单问题了,只需要使用两个变量,分别保存F(N-2)与F(N-1)即可。计算时从下往上计算。代码如下:
/*斐波那契数列计算*/
int Fibonacci(int N)
{
if(N<=1)
return 1;
int last, nextToLast, Answer;
last = nextToLast =1;
for(int i=1; i<N; i++)
{
Answer = last+nextToLast;
nextToLast = last;
last = Answer;
}
return Answer;
}
四、递归关系求解:
这个递归关系是在第七章中遇到过的,关系如下:
C(N)=(2/N)(C(0) + C(1) + ... +C(N-1))+N思路与斐波那契数列计算相同,从低往高计算:
double Eval(int N)
{
double lastSum, Answer;
Answer = lastSum = 1.0;
int i=1;
while(i<=N)
{
Answer = 2.0/i*lastSum+i;
lastSum += Answer;
i++;
}
return Answer;
}
五、矩阵乘法顺序:
问题描述:
给定n个矩阵:A1,A2,...,An,其中Ai与Ai+1是可乘的,i=1,2...,n-1。确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。输入数据为矩阵个数和每个矩阵规模,输出结果为计算矩阵连乘积的计算次序和最少数乘次数。
这个问题难度就上升了不少,不过同样,可以先利用递归思想,得到其递归的关系,然后再去考虑是否需要使用动态规划来优化,
递推关系:
设计算A[i:j],1≤i≤j≤n,所需要的最少数乘次数m[i,j],则原问题的最优值为m[1,n]。
当i=j时,A[i:j]=Ai,因此,m[i][i]=0,i=1,2,…,n
当i<j时,若A[i:j]的最优次序在Ak和Ak+1之间断开,i<=k<j,则:m[i][j]=m[i][k]+m[k+1][j]+pi-1pkpj。由于在计算是并不知道断开点k的位置,所以k还未定。不过k的位置只有j-i个可能。因此,k是这j-i个位置使计算量达到最小的那个位置。
综上,有递推关系如下:

有了这个递归关系,我们就可以尝试使用递归的方式来求解这个问题了。
递归方法:
显然使用递归方式,需要进行一个for循环来寻找m[i,j]的最优值,伪代码如下:
int OptMatrix(Matrix array, int left, right)
{
int min;
int temp;
for(int k= left , k<right, k++)
{
temp = OptMatrix(array, left, k)+OptMatrix(array, k+1, right)+ P[left-1]*P[k]*P[right];
if(temp< min)
min = temp;
}
return min;
}大致就是如上的过程(省略的边界条件),从I到j之间循环一次,找到最小值,返回给上一层的递归调用。但是,很显然,这样做会导致同一个最优顺序被计算很多次。因此这里就需要使用动态规划来求解了。
非递归方法:
在之前的做法是只使用几个变量,保存下计算下一个值的所需要的变量,在这里,显然不行。因为计算N个矩阵相乘,可以划分成1*(N-1)到(N-1)*1,所以中间每一个组合都必要要保存。因此必须使用一个矩阵,或者说二维数组来保存对应的最优解了。
保存方式:
M[i][j]中保存计算从i-j中的最优乘法顺序所用的乘法次数,P[i][j]中,保存分割点,比如为k,代表i-k乘以k+1 - j的分割,有最优解。求解的方式同样是从最低计算到最高,每种情况只需要计算一次。
编码实现:
/*矩阵乘法顺序安排*/
void OptMatrix(const long C[], int N, TwoDimArray M, TwoDimArray LastChange)
{
int i, k, left, right;
long ThisM;
for(left =1; left<=N; left++)
M[left][left] = 0;
for(k=1; k<N; k++)
for(left=1; left<=N-k; left++)
{
right = left+k;
M[left][right] = infinity;
for(i = left; i<right; i++)
{
ThisM = M[left][i]+M[i+1][right] + C[left-1]*C[i]*C[right];
if(ThisM<M[left][right])
{
M[left][right] = ThisM;
LastChange[left][right] = i;
}
}
}
}
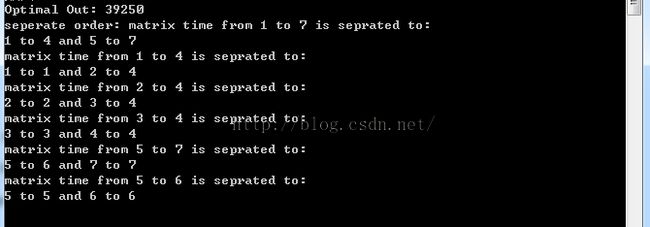
测试结果:
这里的测试结果与预设相同,输出时也输出了矩阵划分的顺序。
六、最优二叉查找树:
最优二叉查找树:
给定n个互异的关键字组成的序列K=<k1,k2,...,kn>,且关键字有序(k1<k2<...<kn),我们想从这些关键字中构造一棵二叉查找树。对每个关键字ki,一次搜索搜索到的概率为pi。可能有一些搜索的值不在K内,因此还有n+1个“虚拟键”d0,d1,...,dn,他们代表不在K内的值。具体:d0代表所有小于k1的值,dn代表所有大于kn的值。而对于i = 1,2,...,n-1,虚拟键di代表所有位于ki和ki+1之间的值。对于每个虚拟键,一次搜索对应于di的概率为qi。要使得查找一个节点的期望代价(代价可以定义为:比如从根节点到目标节点的路径上节点数目)最小,就需要建立一棵最优二叉查找树。
这里,我们定义一个访问代价,构造树使得访问代价达到最小:
根节点深度为1,下面依次递增。
现在给出一个节点概率已经可能的二叉树:
如上图所示,是课本中给出的例子所构建的二叉树,表格中是各个节点出现的概率。其中,第三棵树时最优的。为了求解,我们再次构造一个地推关系,一个搜索二叉树是有左树,右树,加上根节点组成,那么递归关系如下:
其中,Cleft代表整个新构成的树,Pi代表新的根节点,Cleft,i-1为左树,Ci+1, right为右树,左树和右树加上根节点构成新的树时,左右树的每个节点的深度加上了1,所以需要再加上左右树中所有节点的概率。
有了这个关系,我们就可以开始编写求解最优二叉树的代码了,大家应该已经注意到,这个递归关系与之前的矩阵最优乘法顺序很相似,因此,可以使用同样的存储方式来保存结果。
编码实现:
编码时需要注意,因为允许左树或者右树为0 的情况出现,所以需要进行判断,当left>right的时候,返回0。
double sum(const Vob C[], int left, int right)
{
double output = 0;
for(int i=left; i<= right; i++)
output += C[i].value;
return output;
}
double value(doubleArray M, int left, int right)
{
if(left>right)
return 0.0;
return M[left][right];
}
/*最优查找二叉树,为了保持和上面的最佳矩阵乘法顺序形式相同,这里计数也从1开始,0没有定义*/
void OptSearchTree(const Vob C[], int N, doubleArray &M, TwoDimArray &LastChange)
{
int left, right, k;
double ThisM;
for(int i=1; i<=N; i++)
M[i][i] = C[i].value;
for(k=1; k<N; k++)
for(left =1; left<=N-k; left++)
{
right = left+k;
M[left][right] =infinity;
for(int i=left; i<=right; i++)
{
ThisM = value(M, left, i-1) + value(M, i+1, right)+sum(C, left, right);
if(ThisM < M[left][right])
{
M[left][right] = ThisM;
LastChange[left][right] = i;
}
}
}
}
测试结果:
所得的结果与贴出来的最优二叉树相同。
总结:
我最初一直以为,递归转非递归只不过是实现方式的不同罢了,也知道递归变成非递归会有性能的提升,不过我过去一直以为是只会少了压栈的内存而已。没有想到会有如此大的性能提升,因此,以后遇到递归的问题,必须先要分析清楚,其递归调用的开销,是否是指数增长,同一个问题会求解多次的递归。如果是的,就一定需要利用动态规划的方式来编码了。