《数据结构与算法分析》网络最大流问题

前言：

      网络流最大流的实现也是对前面所学的知识的一次总结，这一部分内容书本没有给出任何的代码或者伪代码，只用画图的方式叙述了一下整个过程的思想。实现的细节就是完全根据所学的内容，利用之前的实现数据结构完成。在完成这一部分编码的过程时，还发现了我以前对邻接表实现的缺陷，内聚耦合做的不够完善，需要独立成函数的模块不够独立。在实现的过程中我重新修改了邻接表的程序模块。

我的github：

我实现的代码全部贴在我的github中，欢迎大家去参观。

https://github.com/YinWenAtBIT

介绍：

网络最大流：

一、定义：

在给定边容量的有向图中，找到从发点（source）到收点（sink）之间可以存在的最大网络流。

二、Edmond-Karp算法：

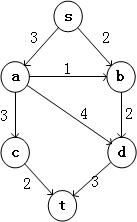
首先建立一个网络流图，图的每条边代表可以经过该边的流量。这里使用图片为P232页的例子。

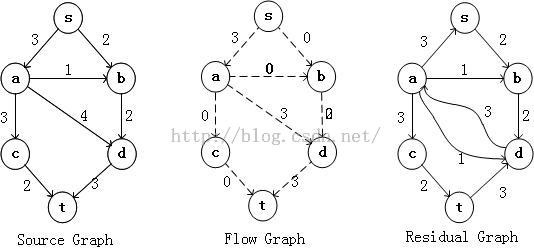
1. 建立一个空的Gf图，作为流图

2. 建立一个残余图Gr，残余图初始化与给定的网络流图相同。

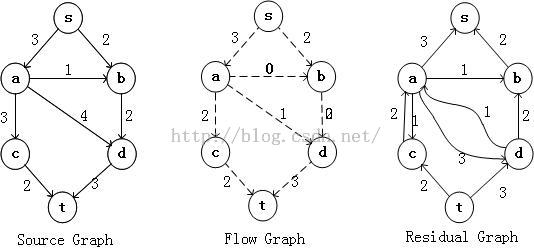
3. 在残余图上使用BFS算法寻找增广路径，如果找到，则使用该路径上的最小流值修改Gr与Gf图。

4. 重复过程3，直到无法找出能从发点到收点的增广路径。此次流图Gf为所求。

使用下图来标出每一个过程中Gr与Gf图的变化：

编码实现：

数据结构：

为了实现这个过程，最重要的部分是如何保存流图，残余图，以及如何求增广路径。

1.保存流图，残余图，还可以使用邻接表，路径上的权值用来代表流量，流量改变时在权值上进行相应的修改，当权值为0时删去该边。

2.求增广路径可以使用BFS遍历的方式，唯一不同之处在于，遍历中表结构的元素dv不再记录路径长度，改为记录该路径上最小的流量。初始化表时，起点的dv元素不再置为0，保持为无穷大。不然会导致每一条路径的dv都变为0。

有了这个思路之后，我们不需要添加新的数据结构，使用原有的邻接表和路径表就可以完成整个计算过程。

函数与预定义：

#define MIN(x,y) ((x)<(y)?(x):(y))

Graph copyGraph(Graph D, Graph S);
void copyVertex(Graph D, Graph S);
void maxStream(Index S, Index E, Graph Gf, Graph Gr);
void modifyGraphByIncrem(Index E, Table T, Graph Gf, Graph Gr);
void getShortestIncrePath(Index S, Table T, Graph G);
void modifyWeightGr(Index V, Index W, WeightType weight, Graph Gr);
void modifyWeightGf(Index V, Index W, WeightType weight, Graph Gf);
void decreaseWeight(Index V, Index W, WeightType weight, Graph Gr);
void increaseWeight(Index V, Index W, WeightType weight, Graph Gr);
bool isEdgeExist(Index V, Index W, Graph G);

准备Gr与Gf图：
先找到顶点对应的序号，然后把输入的网络流图复制给Gr，需要利用复制函数copyGraph。准备好了Gr与Gf图之后就可以开始处理过程了。

Graph maxStream(VertexType source, VertexType sink, Graph G)
{
	Index S = findVertex(source, G);
	Index E = findVertex(sink, G);
	if(G->TheCells[S].Info != Legitimate || G->TheCells[E].Info != Legitimate)
	{
		fprintf(stderr, "vertex %s or %s does not exist", source, sink);
		return NULL;
	}
	/*准备好残余图和流图*/
	Graph Gr = intializeGraph(G->vertex);
	Gr = copyGraph(Gr, G);
	Graph Gf = intializeGraph(G->vertex);
	copyVertex(Gf, G);

	
	maxStream(S, E, Gf, Gr);
	DestroyGraph(Gr);

	return Gf;
}

处理核心：

核心算法部分为在Gr图中找到一条增广路径，然后利用返回的路径表中的路径与网络流来修改Gr与Gf图，直到最后没有从发点到收点的增广路径。

void maxStream(Index S, Index E, Graph Gf, Graph Gr)
{
	/*生成列表*/
	Table T = (Table)calloc(Gr->vertex, sizeof(TableNode));
	if(T == NULL)
	{
		fprintf(stderr, "not enough memory");
		return;
	}
	/*初始化表，并且计算第一条增广路径*/
	initTable(S, Gr->vertex, T);
	getShortestIncrePath(S, T, Gr);
	/*运算直到没有增广路径*/
	while(T[E].dist != Infinity)
	{
		modifyGraphByIncrem(E, T, Gf, Gr);
		initTable(S, Gr->vertex, T);
		getShortestIncrePath(S, T, Gr);
	}
}

根据路径表修改Gr、Gf图：

对于Gr与Gf修改办法不同。Gr删去的流量需要在反方向加回来。Gf在一个方向上增加流量，需要先判断反方向是否已经有一条边。

void modifyWeightGr(Index V, Index W, WeightType weight, Graph Gr)
{
	/*Gr图中，先减去从V->W路径上权值weight,
	如果减去后权值为0，则删去这条边*/
	decreaseWeight(V, W, weight, Gr);

	/*然后在W->V这条路径上增加权值weight,
	如果边不存在，则添加这条边*/
	increaseWeight(W, V, weight, Gr);
}

void modifyWeightGf(Index V, Index W, WeightType weight, Graph Gf)
{
	/*先判断相反方向的边是否存在，如果存在,
	则在相反路径上减去权值weight,如果不存在则在该路径上增加权值*/
	if(isEdgeExist(W, V, Gf))
		decreaseWeight(W, V, weight, Gf);
	else
		increaseWeight(V, W, weight, Gf);
}

其他的一些函数就是与我的邻接表相关的具体实现了，在这里就不再贴出来。如果需要全部代码的可以去我的github。
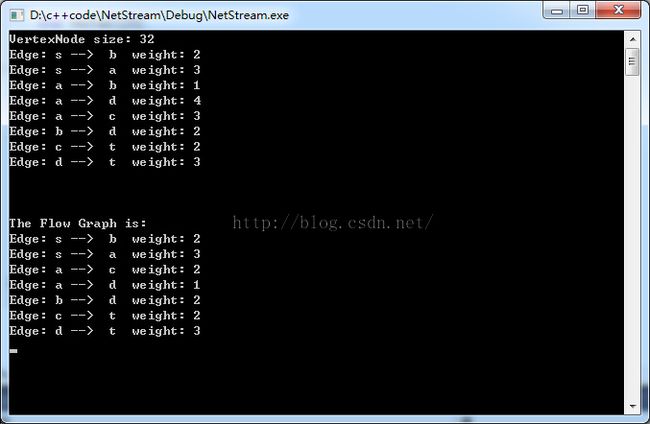
测试结果

输入的流图与上面给出的流图相同，输出的是图的每一条边与边上的加权，因此需要大家对照着图来看输出结果。因此在这里再贴出上面的结果图与原图

总结：

这一部分的实现从阅读这一节到调试完毕，估计用了8个小时左右。确实能感受到自己的编码速度，已经对于程序的设计结构已经有一点领悟了。现在实现一个问题，已经不再需要别人给出伪代码与数据结构了，我已经有能力自己重头完成了。

另外这一次调试时发现的一个问题就是单元测试的重要性。我的哈希函数以及邻接表的实现函数中各有一个不起眼的错误。平时不会出现，当遇到特定的哈希值时，结果就出问题了。这一次调试的时候本来以为是最大流计算函数出错，结果一步步查下去发现是插入边的函数出错了。因此我打算找时间再来学一学如何进行单元测试。