GIS中的WKB介绍
GIS中的WKB介绍
WKB的全称是The Well-known Binary,也简称WKB,OGC与ISO/TC211都做出了同样的规范,它是用来几何体的表达。即用连续的二进制流来表达几何体,这样在GIS互操作方面也有好处。现代GIS软件的底层模块中可以说都有关于WKB解析代码。在二进制存储中有大尾端和小尾端之分,通常在二进制流的第一个字节就指定,这样在这个字节之后的字节流就可以按照相应的大小尾端模式进行解析。分大小尾端是为了适应不同平台环境。在一些开源和商业GIS软件中都支持几何体的WKB表示,这样做也是为了异构平台之间互操作。
基本块的定义如下,这些基本定义在后面的几何体建模中会用到:
Point {
double x;
double y}
PointZ {
double x;
double y;
double z}
PointM {
double x;
double y;
double m}
PointZM{
double x;
double y;
double z;
double m}
LinearRing{
uint32 numPoints;
Point points[numPoints]}
LinearRingZ{
uint32 numPoints;
PointZ points[numPoints]}
LinearRingM{
uint32 numPoints;
PointM points[numPoints]}
LinearRingZM{
uint32 numPoints;
PointZM points[numPoints]}
//字节序
enum WKBByteOrder {
wkbXDR =0, // 大尾端
wkbNDR =1 // 小尾端
}
下面表示几何体的整型的数值,用枚举表示。
enum WKBGeometryType {
wkbPoint = 1,
wkbLineString = 2,
wkbPolygon = 3,
wkbTriangle = 17
wkbMultiPoint = 4,
wkbMultiLineString = 5,
wkbMultiPolygon = 6,
wkbGeometryCollection = 7,
wkbPolyhedralSurface = 15,
wkbTIN = 16
wkbPointZ = 1001,
wkbLineStringZ = 1002,
wkbPolygonZ = 1003,
wkbTrianglez = 1017
wkbMultiPointZ = 1004,
wkbMultiLineStringZ = 1005,
wkbMultiPolygonZ = 1006,
wkbGeometryCollectionZ = 1007,
wkbPolyhedralSurfaceZ = 1015,
wkbTINZ = 1016
wkbPointM = 2001,
wkbLineStringM = 2002,
wkbPolygonM = 2003,
wkbTriangleM = 2017
wkbMultiPointM = 2004,
wkbMultiLineStringM = 2005,
wkbMultiPolygonM = 2006,
wkbGeometryCollectionM = 2007,
wkbPolyhedralSurfaceM = 2015,
wkbTINM = 2016
wkbPointZM = 3001,
wkbLineStringZM = 3002,
wkbPolygonZM = 3003,
wkbTriangleZM = 3017
wkbMultiPointZM = 3004,
wkbMultiLineStringZM = 3005,
wkbMultiPolygonZM = 3006,
wkbGeometryCollectionZM = 3007,
wkbPolyhedralSurfaceZM = 3015,
wkbTinZM = 3016,
}
以下就是各个几何体的定义了。
(1) 点
主要包括字节序和几何体类型,接着后面是坐标总共是1+4+16=21个字节
WKBPoint{
byte byteOrder; //字节序
static uint32 wkbType= 1; //几何体类型
Point point} //点的坐标
WKBPointZ{
byte byteOrder;
static uint32 wkbType = 1001;
PointZ point}
WKBPointM{
byte byteOrder;
static uint32 wkbType= 2001;
PointM point}
WKBPointZM{
byte byteOrder;
static uint32 wkbType= 3001;
PointZM point}
(2)线串,即折线
WKBLineString{
byte byteOrder; //字节序
static uint32 wkbType = 2; //几何体类型
uint32 numPoints; //点的个数
Point points[numPoints]} //点的坐标数组
总的字节大小
1+4+4+ numPoints*sizeof(Point)字节
WKBLineStringZ{
byte byteOrder;
static uint32 wkbType = 1002;
uint32 numPoints;
PointZ points[numPoints]}
WKBLineStringM{
byte byteOrder;
static uint32 wkbType= 2002;
uint32 numPoints;
PointM points[numPoints]}
WKBLineStringZM{
byte byteOrder;
static uint32 wkbType= 3002;
uint32 numPoints;
PointZM points[numPoints]}
(2) 多边形
所占的字节大小是:1+4+4+ numRings*(4 + LinearRing.numPoints*sizeof(Point))
WKBPolygon{
byte byteOrder; //字节序
static uint32 wkbType= 3; //几何体类型
uint32 numRings; //线串的个数
LinearRing rings[numRings]} //线串(环)的数组
WKBPolygonZ{
byte byteOrder;
static uint32 wkbType= 1003;
uint32 numRings;
LinearRingZ rings[numRings]}
WKBPolygonM{
byte byteOrder;
static uint32 wkbType = 2003;
uint32 numRings;
LinearRingM rings[numRings]}
WKBPolygonZM{
byte byteOrder;
static uint32 wkbType = 3003;
uint32 numRings;
LinearRingZM rings[numRings]}
(4)三角形注:当前主流GIS软件中把这个放在TIN中建模
WKBTriangle{
byte byteOrder; //字节序
static uint32 wkbType= 17; //几何体的类型
uint32 numRings; //环的个数
LinearRing rings[numRings]} //环的数组
WKBTriangleZ{
byte byteOrder;
static uint32 wkbType= 1017;
uint32 numRings;
LinearRingZ rings[numRings]}
WKBTriangleM{
byte byteOrder;
Static uint32 wkbType= 2017;
uint32 numRings;
LinearRingM rings[numRings]}
WKBTriangleZM{
Byte byteOrder;
static uint32 wkbType= 3017;
uint32 numRings;
LinearRingZM rings[numRings]}
(5)多面体表面
WKBPolyhedralSurface{
bytebyteOrder; //字节序
staticuint32 wkbType = 15; //几何体类型
uint32numPolygons; //多边形数目
WKBPolygonpolygons[numPolygons]} //多边形的数组
WKBPolyhedralSurfaceZ{
bytebyteOrder;
staticuint32 wkbType=1015;
uint32numPolygons;
WKBPolygonZpolygons[numPolygons]}
WKBPolyhedralSurfaceM{
bytebyteOrder;
staticuint32 wkbType=2015;
uint32numPolygons;
WKBPolygonMpolygons[numPolygons]}
WKBPolyhedralSurfaceZM{
bytebyteOrder;
staticuint32 wkbType=3015;
uint32numPolygons;
WKBPolygonZMpolygons[numPolygons]}
(6)不规则三角网(TIN)貌似一般三角网和矢量数据的几何模型位于同一层次上,所以目前很少看到有GIS软件这样建模的。仅仅是自己的观点
WKBTIN {
bytebyteOrder; //字节序
staticuint32 wkbType = 16; //几何体的类型
uint32numPolygons; //多边形的数目
WKBPolygonpolygons[numPolygons]} //多边形数组
WKBTINZ{
bytebyteOrder;
staticuint32 wkbType=1016;
uint32numPolygons;
WKBPolygonZpolygons[numPolygons]}
WKBTINM{
bytebyteOrder;
staticuint32 wkbType=2016;
uint32numPolygons;
WKBPolygonMpolygons[numPolygons]}
WKBTINZM{
bytebyteOrder;
staticuint32 wkbType=3016;
uint32numPolygons;
WKBPolygonZMpolygons[numPolygons]}
(7)多点
WKBMultiPoint{
byte byteOrder; //字节序
staticuint32 wkbType=4; //几何体类型
uint32 numPoints; //点的个数
WKBPoint points[numPoints]} //点的数组
WKBMultiPointZ{
Byte byteOrder;
Static uint32 wkbType=1004;
uint32 numPoints;
WKBPointZ points[numPoints]}
WKBMultiPointM{
byte byteOrder;
static uint32 wkbType=2004;
uint32 numPoints;
WKBPointM points[numPoints]}
WKBMultiPointZM{
byte byteOrder;
Static uint32 wkbType=3004;
uint32 numPoints;
WKBPointZM points[numPoints]}
(8)多线串
WKBMultiLineString{
byte byteOrder; //字节序
staticuint32 wkbType = 5; //几何体类型
uint32 numLineStrings; //线串的个数
WKBLineString lineStrings[numLineStrings]} //线串数组
WKBMultiLineStringZ{
byte byteOrder;
static uint32 wkbType= 1005;
uint32 numLineStrings;
WKBLineStringZ lineStrings[numLineStrings]}
WKBMultiLineStringM{
byte byteOrder;
static uint32 wkbType = 2005;
uint32 numLineStrings;
WKBLineStringM lineStrings[numLineStrings]}
WKBMultiLineStringZM{
byte byteOrder;
static uint32 wkbType = 3005;
uint32 numLineStrings;
WKBLineStringZM lineStrings[numLineStrings]}
(9)多多边形
WKBMultiPolygon{
bytebyteOrder; //字节序
staticuint32 wkbType = 6; //几何体类型
uint32numPolygons; //多边形数目
WKBPolygonpolygons[numPolygons]} //多边形数组
WKBMultiPolygonZ{
bytebyteOrder;
staticuint32 wkbType = 1006;
uint32numPolygons;
WKBPolygonZpolygons[numPolygons]}
WKBMultiPolygonM{
bytebyteOrder;
staticuint32 wkbType = 2006;
uint32numPolygons;
WKBPolygonMpolygons[numPolygons]}
WKBMultiPolygonZM{
bytebyteOrder;
staticuint32 wkbType = 3006;
uint32numPolygons;
WKBPolygonZMpolygons[numPolygons]}
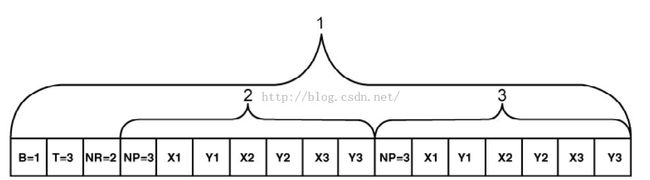
下图是一个多边形的WKB布局。该图表示这个多边形的WKB存储是小尾端,有两个环,并且两个环的点的个数都是3。