Screen Space Ambient Occlusion(SSAO)
1. 简介
AO(Ambient Occlusion)是全局光照中(Global Illumination)中一个很重要的概念,主要用来描述物体间的相互遮挡关系 以及漫射光线之间相互作用的效果。AO的主要方法是在每个采样点上计算它被其它几何体元遮挡的程度,进而得到在一个统一的光照强度下场景中的软阴影效果的图形算法。一般的3D处理软件中均有该算法提供,但是所有这些都是基于离线的渲染,直到在CryTek提出了Screen Space Ambient Occlusion(SSAO)之后。它通过使用后处理渲染中的一些常用信息(如Depth, Position等)将传统的基于3D空间的AO计算转换到完全基于2D屏幕空间的操作,大大提高了计算效率,而且得到了很不错的渲染效果,进而使得这样一个重要的技术在游戏中的应用变得可行。现在SSAO已经是每个主流引擎必备的一个后处理特效。
2. 原理
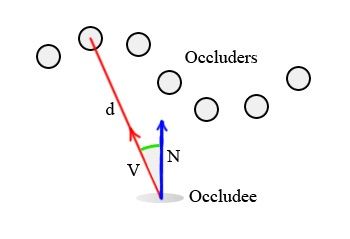
传统的AO实现方法通常是使用光线跟踪的来完成。通过从每个可视点发出若干条光线 ,并与全局的场景进行相交测试来得到相应点的AO值。这些发出的光线通常是在目标点的法向量所决定的一个半球空间内(与之对应的另外半球内没有贡献)。典型的AO计算公式如下所述:
其中的n表示几何体元在P点外所对应的法向量,V为相应的可见函数,![]() 表示对应的半球空间,
表示对应的半球空间,![]() 表示半球体
表示半球体![]() 从P点处射出的方向向量。AO值的计算通过对围绕P点的半球体上的局部AO值进行积分而得到,由此可见函数V为二值函数,即其可能值为0或1,分另表示在从P点处在n方向上不可以或可以看到环境中的其它几何体。
从P点处射出的方向向量。AO值的计算通过对围绕P点的半球体上的局部AO值进行积分而得到,由此可见函数V为二值函数,即其可能值为0或1,分另表示在从P点处在n方向上不可以或可以看到环境中的其它几何体。
另外,上式中的积分表达意味着在理想情况下需要发射出无数条光线来完成当前点的AO值计算,而这在实践中是不可行的,即便是PBRT中,因而需要将其离散化以变得具有可行性(如使用Monte Carlo积分变换)
经过这样离散化操作之后,该算法就已经具有可行性了,如果手边有一个光线跟踪渲染引擎的话只需将上述公式实现后并结合随机采样就可以实现一个较高质量的AO渲染。但是对于游戏中需求的实时渲染来说的话同样不可行,因而这样基于3D空间计算的代价仍然很大,这也就是SSAO产生的原因。
3. Crytek SSAO
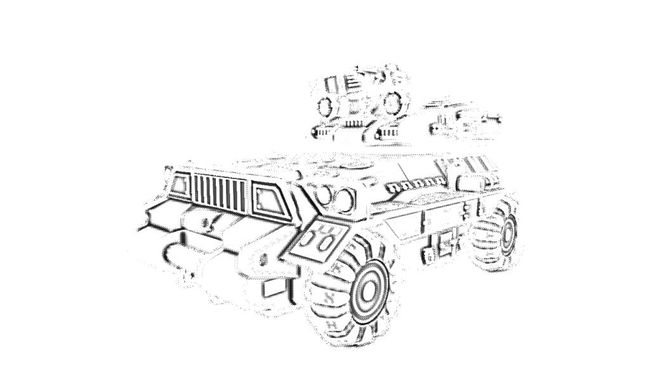
Crytek最早提出了基于屏幕空间的AO算法,因此就称之为SSAO。在此之后与之类似或不同方面改进行的SSAO算法不断涌现。其算法实现较为简单直白:首先,提供一张存储随机向量的纹理,然后在PS中通过这些随机向量构造出3D空间中的随机采样点;通过2D投影并采样深度纹理得到这些对应的采样点处的深度值;比较采样点处的深度值与目标片元处的深度值间的关系并做AO值的计算。该算法的详细描述可见于Shader X7中的论文(Shader X7 Article 6.1)。其SSAO效果可见下图所示。
当然,在最新的Crytek引擎中,原始的SSAO算法还是得到了不少的改进。比如downscaled的Z-Buffer。对线性的Z值进行编码并存储到一个ARGB8(32bits)的Texture中,这样可以减少RT的位宽,同时又不会降低Z值的精度(事实证明存储Z值的位宽不够的话会出现很多Z-fighting带来的dirty效果,而且很难用blur消除)。此外,对于SSAO的计算是在half-size的屏幕分辨率上进行的,这样计算的代价就可以减少为原来的1/4。同时,采样的基本方法也不再用原始的随机空间点采样,而也采用VO(Volumetric Obscruance,下述)中的体积采样,并成功地将采样点的数目减少到了4个(当然,这一点也需要与其另外的一个改进方法Temporal accumualtion结合来使用,否则采样点着实有些少导致效果不理想)。
4. Maria SSAO
这种方法来自于GameDev上的一篇文章(作者名叫Jose Maria Mendez,就姑且叫做Maria SSAO吧 ^o^),比较简单且容易实现,而且效果也不错。但其使用了较多的Buffer信息来完成AO的计算,Normal、Position、Depth(可以说能用的都用上了),因此一般来说这种方法在游戏中不具有太多的实用价值,因为比较慢,且额外信息较多。
不过通过实验结果也可以看出来,这种方法是在不经过Blur情况下噪声最少的一种。而且由于使用了Normal信息,因而对于自遮挡(self-occlusion)的情况处理得比较好(效果图见于后部)。
5. Volumetric Obscurance
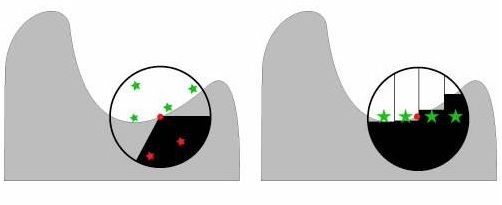
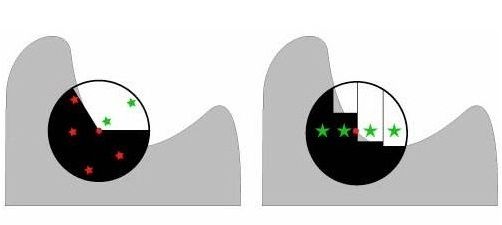
Volumetric Obscurance最早由Loos等人提出来[Paper],应该说在较少的采样点的情况下这种模型比点采样更合理,因为其可以让采样点的利用更加有效。如传统的点采样情况下很可能就会出现两个虽然空间上不同位置的点经过2D投影后会得到重叠在一起(很容易理解),进行做两次相同Z值的采样,对最终的AO值计算贡献重复,这样其实降低了采样点的利用率,同时降低了速度。点采样与体采样的区别可见下图所示。
其实体采样的原理也很容易理解,其实就是相当于对目标几何体元所处的位置上的积分球体,用垂直于视平面的柱体进行分割(积分的原理),当分割无限增多 时我们就可以精确地得到球体的体积。而在计算AO时并不是要得到对应的球体的体积,而是要计算出被计何体元遮挡的部分的体积。
VO原理的2D投影
在Volumetric Obscruance提出之后很多之前基于点采样的SSAO都变成了基于体采样的VO,毕竟其相对于点采样来说可以用更少的采样点得到更好的效果。如最新的CryEngine的SSAO,以及Frostbite2中的SSAO,可见,在以后的引擎中使用VO将会是主流。
6. 其它
基于SSAO的研究最近也比较火热,每年的图形学会议上都会出现不少相应的改进方法出来。比如Alchemy SSAO,这其实是应用于Alchemy引擎中的SSAO算法,作者是在VO的基础上对AO的计算方法作了些许改进,从文中看的话效果是比VO要好一些(但论文中的采样点较VO多),也解决了一些原始VO中的一些问题,比如边缘悬空的AO值等。另外还有SSDO,它将方向性阴影以及间接光照都考虑在SSAO内,但代价就是计算量的增大。在2011年的Siggraph上有几个德国的哥们发了一篇比较有意思的文章,他们将Spherical Harmonic与SSAO结合起来达到SSDO的效果(S3HO)。这里的算法同样是基于屏幕空间的,只不过通过采样得到的几何遮挡信息(由Depth或Geometry)并不是直接用来计算AO,而是用来计算SH系数,然后再将这些系数与传入的光源SH系数对光照进行还原,能得到同样的SSDO的效果。虽然运算速度会比单纯的SSAO要慢一些,不过还是有很大的改进空间的,而且效果要比SSAO好,比SSDO更容易实现与整合。关于S3HO,论文里边讲得很简单,具体的实现还在研究中。
7. Post Blur
在得到SSAO之后,如何blur是一个重要的操作,甚至会在很大程序上决定最终得到的效果,而且Blur算法甚至会消耗与SSAO计算相差无几的时间。传统常用的Blur算法有许多种,比如Gaussian Blur、Possion Blur等,但是在这里SSAO使用的算法有一个很重要的额外要求,那就是边界保持(Edge Preserving)。这就需要用到Bilateral Blur(当然传统的Gaussian Blur也可以使用,但是需要加上bilinear来保持边缘,Frostbite2就是用的这种方法),关于这一部分下次再讨论,现在手边只实现有普通的Gaussian Blur。
欢迎交流~~~
以下为一些结果图:
Color Normal
Position Depth
Crytek SSAO Crytek SSAO(Blur)
Maria SSAO Maria SSAO(Blur)
Volumetric Obscurance Volumetric Obscurance(Blur)
以下为针对Sponza的效果图:
Color
CryTek SSAO
Maria SSAO
Volumetric Obscurance