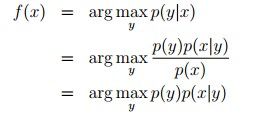NLP 学习笔记 02 (Tagging Problems, and Hidden Markov Models)
(all content based on the coursera course nlp)
--------------------------------------------------------------------------------------------------------
这一周的主要课程是tagging problems
首先是简单介绍了一下supervised learning problem,则是机器学习中的基础了,请参看我写的其他的笔记
介绍了两个模型
Conditional models:
我们从对样例的学习得到一个分布:p(y|x),然后用这个分布来对我们新的数据进行标记
可以很直观地感觉到这个分布的意义:给定一个数据x,它的标记为y的概率。
Generative Models:
我们从样例中学习到一个分布p(x,y),因为有![]()
所以:
对这个模型的直观感受就是:标记y的概率乘以标记y生成数据x的概率,所以它叫做生产模型
Trigram Hidden Markov Models (Trigram HMMs)
对于一句话x,我们对其标记为y,对其用Generative Models进行定义:
那么最有可能的标记y就是:
使用HMM对p(x,y)进行定义,使用trigram模型,则有:
其中的q是在之前笔记定义了的parameter
e(xi | yi)表示标记yi生产xi的概率,一般对样例中得数据进行统计就行了,它等于(xi标记为yi的数量) / (标记yi的数量).
即是:
Dealing with Low-Frequency Words
这个模型一个显著的缺点就是有些词出现的次数极少,那么课程给出的一个解决方法就是对出现次数少的词语进行分类,把分到一类的词语都用特定单词表示,这样出现次数累积起来就多了。
比如说:
分类完成后将所有的两位数字换成 twoDigitNum,四位数字换成fourDigitNum,诸如此类,然后把训练数据中的都替换掉,这样将它们的出现次数累积起来,次数自然就变多了。
The Viterbi Algorithm
定义号这样一个模型之后,我们要解决的问题就是用一个算法来得到结果
单纯的枚举在这里明显是不明智的,这里介绍一个Viterbi Algorithm,实际上是一个动态规划算法,理解起来并不难
首先定义:
Sk表示的是在位置k可选的标号,0和-1自然只能选开始符号,其它可以任意选择所有的标号
定义:
这是对上面的一个重定义,换了个符号而已。
定义:
![]()
π(k,u,v)是在位置k,以u,v结尾的最大的概率,也就是![]() 时的最大概率
时的最大概率
算法:
在π上进行动态规划算法,通过最开始最明显的(下式)进行递推
![]()
推导式为:
我想这个理解起来应该是不难的吧2,一个动态规划而已,下面是伪代码: