计科1111-1114班第四周讲义、课外作业(截止日期:2014年4月3日23点-周四晚,学委飞信通知同学)
第四周主要讲授了 "第3章:图的分解"。首先从欧拉的哥尼斯堡七桥模型开始,引出图论的开始;然后介绍了图模型在一些其他领域的应用。
讲授内容
1. 图论的起源:欧拉 的 哥尼斯堡七桥模型,欧拉回路,欧拉通路。延伸开来就是汉密尔顿回路与汉密尔顿通路。大家学习时可以自己总结与比较一下,结合《离散数学》与《数据结构》,首先搞清楚这些概念的定义,然后比较其中的差异,最后给定一个图(Graph,简称G),能够编程计算出欧拉回路的走法等。
2. 图的应用: 地图着色、配对(延伸阅读:世纪佳缘网的创业经历)、数据可视化等。
3. 图的表示方法:主要有两种,邻接矩阵 和 邻接表。了解两种表示法各自的优点与不足。
4. (重点)无向图的深度优先搜索(DFS):给定图G(V,E),以及某一个节点v,能够得到相应的DFS树;掌握树边 与 回边;应用DFS算法计算图的连通分量的个数(思想是什么?);遍历节点时,前序与后序的计数(简单的思想,给我们很多启发)。
5. (重点)有向图的深度优先搜索(DFS):掌握P102图3-7右图的遍历表示方法;掌握边(u,v)中,树边、前向边、回边、横跨边的判断方法,进而判断图是否有回路;没有回路的情况下(有向无环图),计算其节点的线性化(即:拓扑排序)。
6. (补充知识)搜索引擎与PageRank算法。课堂上有限的时间,老师只能让大家“知道”有这些内容,大家可以自己主动多搜集资料,及老师分发的资料,多掌握一些。
下载与链接
1. 图的分解与PageRank算法(I):主要介绍图的分解
2. 图的分解与PageRank算法(II):主要介绍图的应用 与 PageRank算法
3. PageRank算法:原理,其他。
4. 《算法》视频公开课与优秀书籍网站:Algorithms, 4th Edition(下载),《算法导论》
作业要求
1. 请各班学委飞信通知同学完成作业。2. 作业计入平时成绩,计分依据为大家的完成程度——态度(做 / 未做)。老师会根据大家作业的质量选择若干学生进行评论,以及提供个性化教学的依据。请大家依据自身能力,尽可能提供高水平的作业,为提高自身能力全力以赴。
3. 本次作业,老师将会抽查本班学号位于21-30号的同学,请大家相互转告。
作业内容
学习需要不断练习。请大家至少完成下面的练习1,希望有志于走编程道路的同学完成1、2、3。现在的每一分付出,都可以得到10倍以上的回报。计算机科学专业学生比职业培训的学生优势在哪里,在眼界、思想。
1. 图的表示:给定图数据文件(tinyG.txt),计算得到图的邻接矩阵,并把邻接矩阵保存到文件(tinyG_matrix.txt)中。类名:GraphRepresentation。摘自《Algorithms, 4th Edition》P522。博文标题:第四周作业——图的表示
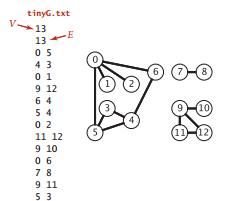
2. 无向图的DFS算法:按照教材中的定义方式,完整实现图的DFS算法,给定图数据文件(tinyG.txt),能够输出DFS的节点遍历结果,及每个节点的Pre和Post值,和连通分量的个数与节点构成。类名:GraphDFS。博文标题:第四周作业——无向图的DFS算法
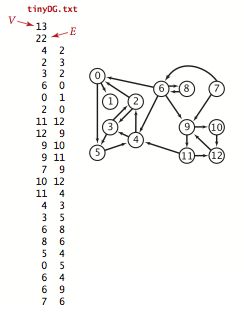
3. 有向无环图的判断:按照教材中对有向无环图(DAG)的定义与判断方式,对图(tinyDG.txt),编程实现并判断该G是否有环,进一步找出环的路径(如:v1-v5-v6-v1)。类名:GraphDAG。摘自《Algorithms, 4th Edition》的部分。博文标题:第四周作业——有向无环图的判断
提前预习
1. 第三章:图的强连通部件(强连通子图)
2. 第四章:图的路径
推荐阅读
大学,我们经常会听到各种各样的建议,从而迷茫。如考证有什么用?公务员需要靠关系?入党能够有助于工作?考试成绩一般找工作都不看?……这些观点都对吗?又错在哪里呢?我们一定需要有自己的判断。人的判断力提升,与自身视野与实践不断丰富有关。
作为大学生,每两周(15天)至少应该阅读一本书,大学3.5年,阅读100本书以上,思考问题的广度与深度就会有质的提升。在这个浮躁的社会里,我们需要有自己的价值判断。虽然已经是大学最后的一年,但一年时间还是可以做很多事情来丰富自己,提升自己的就业竞争力。
本期推荐《逆袭大学——传给IT学子的正能量》、贺利坚老师的博客,看看我们的同龄人都有哪些共同的困惑,及我们走出来的方向与道路。昨晚睡前在思考:没有关系怎么找工作呢?也许,上帝关闭了这扇门,是想让我们透过窗户,看到不一样的风景。有关系,所以我们可以少努力,同时我们可以选择的面也很窄(关系毕竟延伸的面很窄);正因为没有关系,我们需要靠自己的实力与坚韧不拔的精神,不断努力,所以我们能够体验到真实的喜悦与苦涩。年轻就是资本,我们是自己最大的资本。
昨天和几个学生在家聊天,讲到关系,和大家分享一下大一学弟学妹的话:“有一次去医院,听到一个护士说,‘你看,靠关系进来的,就是这样,连这种问题都不会解决’,充满了不屑与轻视。所以,即使靠关系,我们也要提升自己本来的实力,才能够不丢父辈的脸面,站稳自身的脚跟。”。
很抱歉,昨晚11点,没有发布作业。