使用循环坐标下降(CCD)算法解算反向运动学(IK)
使用循环坐标下降(CCD)算法解算反向运动学(IK)
周五的时间总是美好的,今天也将自己制作的演示程序收官了。这篇文章是上一篇文章的继续,向大家介绍一下如何使用循环坐标下降(cyclic coordinatedecent,CCD)算法来求解反向运动学问题。
注意到了没有?我们要解决的问题属于刚体运动学范畴,所以一切涉及到形变的因素都不用考虑,因此我们既可以使用四元数和一个向量表示骨骼的位置和平移,也可以将两者结合起来使用一个矩阵表示骨骼的所有变换。学过计算机图形学的同学都知道,旋转分量和平移分量是互不影响的,所以可以简单地分别将旋转和平移叠加来表示累次旋转和累次平移。
原创文章,反对未声明的引用。原博客地址:http://blog.csdn.net/gamesdev/article/details/14047265
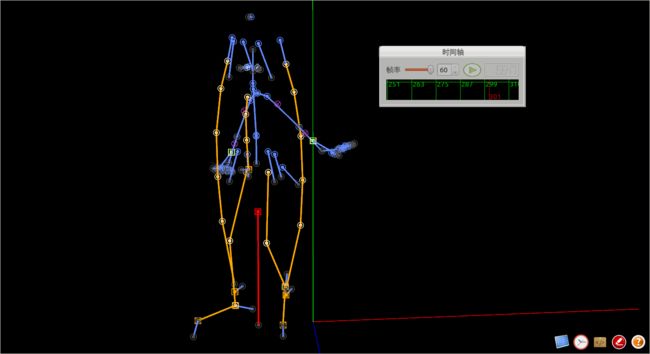
首先让我们看一下同样的场景,当使用反向运动学和不使用反向运动学时的差别:
这是使用了反向运动学的
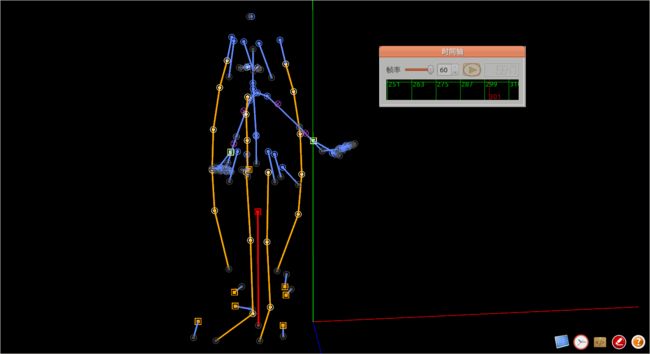
这是未使用反向运动学的,可见初音ミク的腿无法弯曲。
了解了反向运动学的效果之后,我们再看如何用CCD算法来实现反向运动学。
首先让我们来处理最简单的情况:只有两根骨骼、两个关节,这样的情况非常好处理,设原点为origin、目标点为target,用A.relativePos表示A相对于它的父骨骼(也就是origin)的位置,A.finalPos表示A相对于世界坐标系的位置, 如果是正向运动学,那么有:
target.finalPos = origin.finalPos + orgin.rotation * target.relativePos
现在反过来,已知target.finalPos和 origin.finalPos,显而易见,有:
origin.finalPos = target.finalPos – origin.rotation-1 *target.relativePos
解方程,求出origin.rotation即可。
下面来看一下三根骨骼、三个关节的问题怎么求。这种情况多见于人类的手臂部分和腿部分,求解的方法,老实说有两种——使用余弦定理和一般迭代方法。下面我就讲讲使用这两种方式的感受。
使用余弦定理求解见于《Character AnimationWith Direct3D》这本书,余弦定理的公式是C2 =A2+B2-2ABcos(∠C),拿胳膊打比方,当你的胳膊从自然伸直转向弯曲的时候,肘部与肩膀和手掌形成的夹角在缩小。我们拿两个关键帧s和t来进行对比,首先我们知道s帧时手臂的所有位置和方位,这个时候我们可以使用向量点击求出肘部形成的夹角α,其次我们知道t帧时肩膀和手掌的位置,我们需要求出肘部的位置,这时我们可以利用余弦定理,已知两条边长(上臂低位的长度和高位的长度)以及另一条边长(可由手掌的坐标减去肩膀的位置求模得到)以及两个顶点的位置,求出第三个顶点与两个顶点形成的角度β。我们可以计算出δ=β-α。然后根据叉积公式求出旋转轴,将手掌绕着这个旋转轴反向旋转δ就可以近似地到达关键帧t中肘部的位置了。
可是余弦定理只能处理三根骨骼、三个关节的问题,如果是多跟骨骼、多个关节(例如蜈蚣那样),由于概念上的缺陷而无法处理。
一般的迭代方法是这么处理的:
1、从末端关节连接的父关节A开始,计算末端关节与目标末端关节位置与该关节形成的夹角,旋转之;
2、如果旋转后的末端关节未达到目标,则以A的父关节开始重复步骤1;
3、如果到达根关节仍未将末端关节达到目标,则结束一次迭代,重复步骤1、2,进入下一次迭代。
使用迭代的方法是一种传统的解决IK问题的方法,目前出现了几种改进的方法,都是以这种方法为基本,分析其缺陷并加以改进而成的。
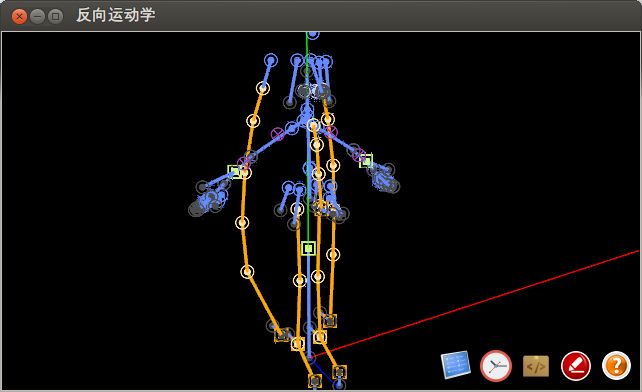
下面是一张演示程序截图,其中初音ミク模型的蓝色骨骼部分是属于正向运动学的,而黄色部分,也就是长发、腿部、脚部和领带则属于反向运动学,受反向运动学影响的骨骼,都受控制端(以同心方块作为标识)的影响。
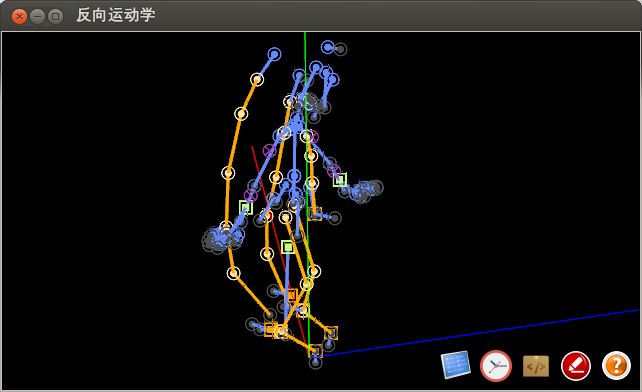
下面是其中的一帧截图,我们发现,角色的腿部和头发部分受到反向运动学的影响而发生弯曲。
下面是使用一般迭代方法处理反向运动学的部分源代码:
/*---------------------------------------------------------------------------*/
void MMDRenderHandler::CalculateInverseKinematics( void )// 计算反向运动学
{
// 遍历每个IK
foreach ( const IK& _IK, m_IKs )
{
Bone& destBone = m_Bones[_IK.destIndex]; // 一般是IK骨骼
Bone& targetBone = m_Bones[_IK.targetIndex]; // 一般是与IK一端连接的骨骼
for ( int i = 0; i < _IK.iteration; ++i )
{
for ( int j = 0; j < _IK.bones.size( ); ++j )
{
quint16 index = _IK.bones[j];
Bone& joint = m_Bones[index];
CCDIKSolve( joint,
targetBone,
destBone,
_IK.limitAngle,
i );
CalculateBonesFinalPos( index );
}
if ( qFuzzyIsNull( ( targetBone.finalPos -
destBone.finalPos ).SquareLength( ) ) )
{
break;// 目的达到了,结束迭代
}
}
}
}
/*---------------------------------------------------------------------------*/
void MMDRenderHandler::CCDIKSolve( Bone& joint, // 想象成肘部
Bone& target, // 目标位置
Bone& end, // 末端效应器
float limitAngle,// 单位限制角度
int iterNum )// 迭代次数
{
// 使用循环坐标下降算法(cyclic coordinate decent,CCD)
// 计算在绝对旋转后的连接点和目标位置以及末端效应器的相对位置
Vector3F absJoint2End = end.finalPos - joint.finalPos;
Vector3F absJoint2Target = target.finalPos - joint.finalPos;
Quaternion invRotation = joint.absRotation.Conjugate( );// 求出四元数的共轭四元数
// 转为本地坐标系(平移因素在第一阶段已剔除)
Vector3F localJoint2End = invRotation.RotatedVector( absJoint2End );
Vector3F localJoint2Target = invRotation.RotatedVector( absJoint2Target );
// 计算应该旋转的角度
float deltaAngle = acosf( Vector3F::DotProduct(
localJoint2End.Normalized( ),
localJoint2Target.Normalized( ) ) );
if ( std::isnan( deltaAngle ) ||
qFuzzyIsNull( deltaAngle ) )// 角度计算出错或角度太小(一般是向量太接近)
{
return;// 不处理,直接返回
}
// 限制角度为[-limitAngle, limitAngle]
deltaAngle = qBound( -limitAngle, deltaAngle, limitAngle );
// 求出旋转轴
Vector3F rotateAxis = Vector3F::CrossProduct( localJoint2Target,
localJoint2End );
// 构造旋转四元数
Quaternion deltaRotation = Quaternion::FromRotation(
rotateAxis, deltaAngle );
joint.rotation *= deltaRotation;
joint.absRotation = m_Bones[joint.parent].absRotation * joint.rotation;
}
/*---------------------------------------------------------------------------*/
演示程序下载地址:这里