DoglegMethod——“狗腿”算法(上)
参考文献:“Numerical Optimization” ---Page71 Dogleg Method
Author:Jorge Nocedal & Stephen J. Wright
问题来源:对于最速下降法,本质的等式在于x(k+1) = x(k) + a(k)*d(k),x(k)为定义域上的点,a(k)为前进的步长,是一个标量,d(k)是前进的方向, 对于高维变量d(k)就是矢量,是一个列向量。一般常用的是取d(k)为x(k)点负梯度方向,当然也可以用到海森阵,就是跟牛顿法很像的一系列算法。
非线性优化的问题本质在于如何寻找合适的a(k)和d(k)(这个本质仅仅是一个初学者看来的)。
参考文献中首先讲解的如何选取步长a(k),然后讲解如何选取方向d(k),由于老师的作业仅仅是布置了选取方向d(k)的一种方法——Dogleg算法的编程,所以这里仅仅贴出如何选取d(k)的一种方法Dogleg算法的代码,其中步长的选取非常粗糙,用了指数衰减的方法,但是由于优化的函数是一个严格凸的,所以步长的选取方法并不需要太过关心。
所优化的函数为[x1,x2] = argmin(100*(x2-x1^2) )^2 + (1-x1)^2)
dogleg.m文件的代码
clear;clc
x1 = 0:0.005:1;
x2 = 0:0.008:2;
ff = zeros(length(x1), length(x2));
for i = 1 : length(x1)
ff(i, :) = 100 * (x2 - x1(i)^2).^2 + (1 - x1(i))^2;
end
x = [min(x1) + (max(x1) - min(x1)) * rand(1), min(x2) + (max(x2) - min(x2)) * rand(1)]';
a = 2;
d = -B(x)^-1 * g(x);
maxiter = 1000;
iter = 1;
rey = [];
rex1 = [];
rex2 = [];
while iter < maxiter
rey = [rey, f(x)];
rex1 = [rex1, x(1)];
rex2 = [rex2, x(2)];
if sum(abs(g(x))) < 0.00001
break
end
iter = iter + 1;
du = -g(x)' * g(x) * g(x) / (g(x)' * B(x) * g(x));
dB = -B(x)^-1 * g(x);
if a < 1
d = a * du;
else
d = du + (a - 1) * (dB - du);
end
if f(x) > f(x + d)
x = x + d;
else
a = a * 0.995;
end
end
hold on
mesh(x2, x1, ff);
plot3(rex2, rex1, rey,'r','linewidth', 4)
f.m 文件
function y = f(x)
y = 100 * (x(2) - x(1)^2)^2 + (1 - x(1))^2;
end
g.m 文件
function y = g(x)
y = [400 * (x(1)^2 - x(2)) * x(1) + 2 * (x(1) - 1), 200 * (x(2) - x(1)^2)]';
end
B.m文件
function y = B(x)
y = [400 * (3*x(1)^2- x(2)) + 2, -400 * x(1);...
-400 * x(1), 200];
end
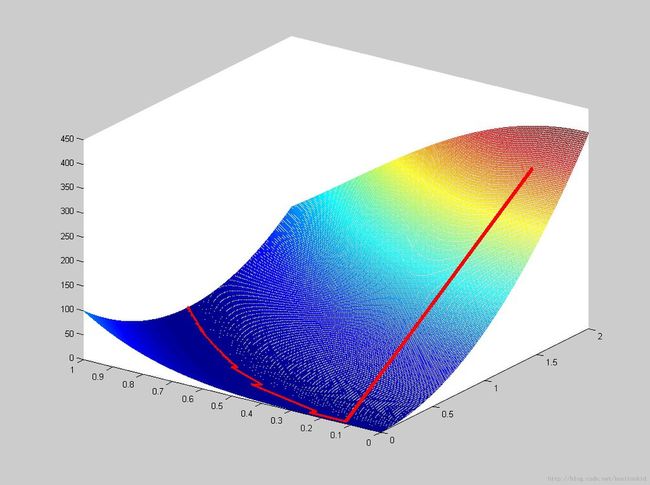
运行结果
红色线是xk的移动方向,蓝色区域是代表着目标函数的低洼地带,最终xk收敛于函数的局部极小值点(这个函数的局部极小值就是全局极小值)
仍然存在的问题
1. 上课没有认真听= =,初始步长a是怎么选的我没记到笔记了,而且文献里也没有……
2. 对于不知道函数关系式的梯度和海森阵该如何求解?是不是用f'(x) = ( f(x+t)-f(x) ) / t ; t->0 这样的原理?
等下周上课再问问老师吧~