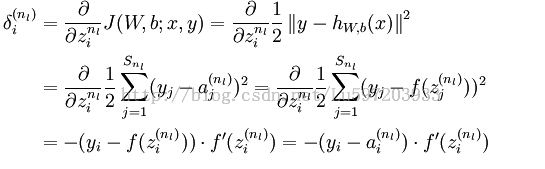UFLDL教程笔记及练习答案四(建立分类用深度学习---栈式自编码神经网络)
此次主要由自我学习过度到深度学习,简单记录如下:
(1)深度学习比浅层网络学习对特征具有更优异的表达能力和紧密简洁的表达了比浅层网络大的多的函数集合。
(2)将传统的浅层神经网络进行扩展会存在数据获取、局部最值和梯度弥散的缺点。
(3)栈式自编码神经网络是由多层稀疏自编码器构成的神经网络(最后一层采用的softmax回归或者logistic回归分类),采用逐层贪婪的训练方法得到初始的参数,这样在数据获取方面就可以充分利用无标签的数据。通过逐层贪婪的训练方法又称为预训练,然后可以使用有标签的数据集对其进行微调。
习题答案:
(1) %% STEP 2: Train the first sparse autoencoder
addpath minFunc/
options.Method = 'lbfgs'; % Here, we use L-BFGS to optimize our cost
% function. Generally, for minFunc to work, you
% need a function pointer with two outputs: the
% function value and the gradient. In our problem,
% sparseAutoencoderCost.m satisfies this.
options.maxIter = 400; % Maximum number of iterations of L-BFGS to run
options.display = 'on';
[sae1OptTheta, cost] = minFunc( @(p) sparseAutoencoderCost(p, ...
inputSize, hiddenSizeL1, ...
lambda, sparsityParam, ...
beta, trainData), ...
sae1Theta, options);
W1 = reshape(sae1OptTheta(1:inputSize*hiddenSizeL1), hiddenSizeL1, inputSize);
display_network(W1', 12);
(2) % STEP 2: Train the second sparse autoencoder
options.Method = 'lbfgs'; % Here, we use L-BFGS to optimize our cost
% function. Generally, for minFunc to work, you
% need a function pointer with two outputs: the
% function value and the gradient. In our problem,
% sparseAutoencoderCost.m satisfies this.
options.maxIter = 400; % Maximum number of iterations of L-BFGS to run
options.display = 'on';
[sae2OptTheta, cost2] = minFunc( @(p) sparseAutoencoderCost(p, ...
hiddenSizeL1, hiddenSizeL2, ...
lambda, sparsityParam, ...
beta, sae1Features), ...
sae2Theta, options);
(3) %% STEP 3: Train the softmax classifier
addpath minFunc/
options.Method = 'lbfgs'; % Here, we use L-BFGS to optimize our cost
% function. Generally, for minFunc to work, you
% need a function pointer with two outputs: the
% function value and the gradient. In our problem,
% softmaxCost.m satisfies this.
minFuncOptions.display = 'on';
lambda = 1e-4;
[saeSoftmaxTheta, cost3] = minFunc( @(p) softmaxCost(p, ...
numClasses, hiddenSizeL2, lambda, ...
sae2Features, trainLabels), ...
saeSoftmaxTheta, options);
(4) %% STEP 5: Finetune softmax model
addpath minFunc/
options.Method = 'lbfgs'; % Here, we use L-BFGS to optimize our cost
% function. Generally, for minFunc to work, you
% need a function pointer with two outputs: the
% function value and the gradient. In our problem,
% softmaxCost.m satisfies this.
minFuncOptions.display = 'on';
[stackedAEOptTheta, cost3] = minFunc( @(p) stackedAECost(p, ...
inputSize, hiddenSizeL2, ...
numClasses, netconfig, ...
lambda, trainData, trainLabels), ...
stackedAETheta, options);
StackedAECost.m
depth = numel(stack);
z = cell(depth+1, 1); %输入+隐藏层的z
a = cell(depth+1, 1); %输入+隐藏层的激励函数
a{1} = data;
for i = 1:depth % 计算隐藏层的z和激励a
z{i+1} = stack{i}.w * a{i} + repmat(stack{i}.b, 1, numCases);
a{i+1} = sigmoid(z{i+1});
end
M = softmaxTheta * a{depth+1}; % 计算softmax对应的激励值
M = bsxfun(@minus, M, max(M, [],1));
M = exp(M); %
p = bsxfun(@rdivide, M, sum(M));
cost = -1/numCases .* sum(groundTruth(:)'*log(p(:))) + lambda/2 *sum(softmaxTheta(:).^2); % cost function
softmaxThetaGrad = -1/numCases .* (groundTruth - p) * a{depth+1}' + lambda * softmaxTheta; % grad softmax对应的参数
delta = cell(depth+1); % 误差项 只需要计算隐藏层的就可以了
delta{depth+1} = -(softmaxTheta' * (groundTruth-p)) .* a{depth+1} .* (1-a{depth+1}); %最后一个隐藏层所对应的error 可以推导出来
for layer = depth: -1: 2
delta{layer} = (stack{layer}.w * delta{layer+1}) .* a{layer} .* (1-a{layer}); %% 计算前面各层所对应的error 没有考虑系数项及贝叶斯学派的参数
end
for layer = depth : -1 :1 % 计算各隐层参数w和b所对应的梯度
stackgrad{layer}.w = delta{layer+1} * a{layer}' ./ numCases;
stackgrad{layer}.b = sum(delta{layer+1}, 2) ./numCases;
end
(5) %% STEP 6: Test
numCases = size(data, 2);
depth = numel(stack);
z = cell(depth+1, 1); %杈撳叆+闅愯棌灞傜殑z
a = cell(depth+1, 1); %杈撳叆+闅愯棌灞傜殑婵?姳鍑芥暟
a{1} = data;
for i = 1:depth % 璁$畻闅愯棌灞傜殑z鍜屾縺鍔盿
z{i+1} = stack{i}.w * a{i} + repmat(stack{i}.b, 1, numCases);
a{i+1} = sigmoid(z{i+1});
end
[~, pred] = max(softmaxTheta * a{depth+1});
最终我得到的结果是:BeforeFinetuning Test Accuracy: 92.150%,After Finetuning Test Accuracy: 96.680% 和练习给的答案有点误差。
下面将反向传播法中进行微调的公式进行推导下:------貌似有误 最后一层softmax计算了激励函数值,不是线性的a=z
声明:个人认为ufldl教程中《微调多层自编码算法》有误:
个人认为不应该说是输出层,应该是最后一个隐藏层,这样后面的公式才是正确的(个人观点)。
由反向传导算法一节中的公式:
由于在此处最后一层softmax回归中,我们并没有求解zi的sigmoid函数,所以:
再由最后一层隐藏层:
最后的结果再矢量化即为代码中的结果,也与教程中给出的公式是一致的。(公式最后一步的f(zi)求导错了,是f(zi)*f(1-zi))