Sicily 解题: 1028 Hanoi Tower Sequence
Hanoi Tower Sequence
Total Submit : 841 Accepted Submit : 212
Problem
Hanoi Tower is a famous game invented by the French mathematician Edourard Lucas in 1883. We are given a tower of n disks, initially stacked in decreasing size on one of three pegs. The objective is to transfer the entire tower to one of the other pegs, moving only one disk at a time and never moving a larger one onto a smaller.
The best way to tackle this problem is well known: We first transfer the n-1 smallest to a different peg (by recursion), then move the largest, and finally transfer the n-1 smallest back onto the largest. For example, Fig 1 shows the steps of moving 3 disks from peg 1 to peg 3.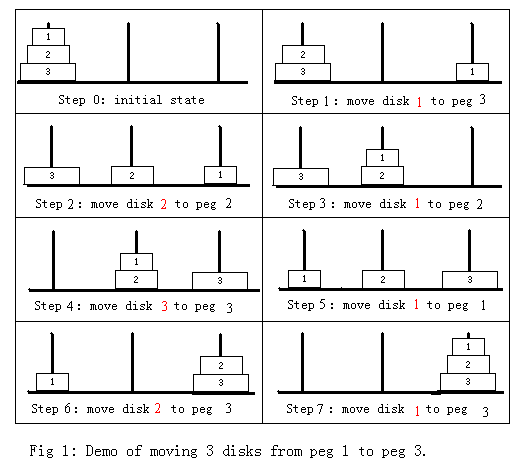
Now we can get a sequence which consists of the red numbers of Fig 1: 1, 2, 1, 3, 1, 2, 1. The ith element of the sequence means the label of the disk that is moved in the ith step. When n = 4, we get a longer sequence: 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1. Obviously, the larger n is, the longer this sequence will be.
Given an integer p, your task is to find out the pth element of this sequence.
Input
The first line of the input file is T, the number of test cases.
Each test case contains one integer p (1<=p<10^100).
Output
Output the pth element of the sequence in a single line. See the sample for the output format.
Print a blank line between the test cases.
Sample input
41
4
100
100000000000000
Sample output
Case 1: 1Case 2: 3
Case 3: 3
Case 4: 15
Problem Source
ZSUACM Team Member
==================================我是华丽的分割线==============================
分析:
序列的第 2 k - 1 + i * 2 k = t * 2k - 1 个数是 k ,i = 1, 2, 3, ... ,t = 1, 3, 5, ...
因此对于输入的正整数 n ,只要计算 n 能被 2 整除的次数,然后输出次数加 1 即可。
使用 109 进制的大整数来表示 n , 可以提高效率。
运行结果:
Run ID User Name Problem Language Status Run Time Run Memory Submit Time
82506 rappizit 1028 C++ Accepted 0 sec 256 KB 2007-09-11 15:16:57
在那道题的排行榜上排第二^_^
Rank Submit Time Run Time Run Memory Language User
1 2005-12-10 01:15:14 0.00S 148K C wangqiang
2 2007-09-11 15:16:57 0.00S 256K C++ rappizit
3 2006-12-22 00:02:44 0.00S 260K C++ jackeyyang
4 2005-04-16 19:16:26 0.00S 264K C++ Savior
5 2006-08-16 00:52:04 0.00S 264K C++ cockerel
==================================我是华丽的分割线==============================
大整数的各个单元是按数组的下标从低到高存放的,即 vli [0] 表示最低 9 位十进制数字。
判断一个整数能否被 2k 整除,等价于整数的最后 k 位十进制数字能被 2k 整除。
1 << k 即为 2k ,a & ((1 << k ) - 1) 即为 a % 2k ,a >> k 即为 a / 2k 。
采用 k = 18。而大整数是 109 进制的,因此判断大整数能否被 2k 整除,只要判断此条件为 true :
((vli [0] + vli [1] * UnitBase) & mask) == 0 ,其中 vli [0] + vli [1] * UnitBase 表示大整数的后 18 位十进制数字,UnitBase = 1,000,000,000 ,mask = (1 << 18 ) - 1 。
PS:这题是算法分析与设计课的第一次作业中的。之前没用109 进制来做,运行时间为 0.06S , 换成109 进制 且使用位运算就为 0.03S ,然后把输入输出换成 scanf , printf 的就为 0.00S !(cin , cout 比较慢。)我稍微修改了一下代码然后用老师指定的 ID (csa+学号)再提交了一次,内存少用了 4K ,再次排在第二名,将原来的 ID rappizit 挤到第三名了,呵呵。。