uva 10313 Pay the Price

题意：有1到300的价值的硬币，给你一个价值，后面跟着一到两个数字，一个数字a表示你要用a枚或者更少的硬币去凑成这个价值，两个数字a，b表示你用a到b范围内的硬币去凑成这个价值。

#include <cstdio>
#include <cstring>
using namespace std;
const int N=305;
#define LL long long
LL map[N][N];
bool vis[N][N];
LL dp(int,int);
int main()
{
    char str[2000];
    while(gets(str))
    {
        int a[3]={0};
        int cnt=sscanf(str,"%d%d%d",&a[0],&a[1],&a[2]);
        if(a[1]>300) a[1]=300;
        if(a[2]>300) a[2]=300;
        if(cnt==1) printf("%lld\n",dp(a[0],a[0]));
        else if(cnt==2) printf("%lld\n",dp(a[0],a[1]));
        else
        {
            if(a[1]>1)printf("%lld\n",dp(a[0],a[2])-dp(a[0],a[1]-1));
            else printf("%lld\n",dp(a[0],a[2]));
        }
    }
    return 0;
}
LL dp(int x,int y)
{
    bool &flag=vis[x][y];
    LL &res=map[x][y];
    if(flag) return res;
    else if(x==0){flag=1;res=1;return res;}
    else
    {
        for(int i=y;i>=1;i--)
        {
            if(x-i>=0) res+=dp(x-i,i);
        }
        flag=1;return res;
    }
}

主要是用到了ferrers图的性质。

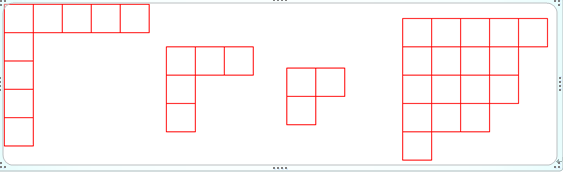
ferrers图：一个从上而下的n层格子，m_i为第i层的格子数，当m_i>m_i+1,（i=1,2,…n-1），即上层的格子数不少于下层的格子数时，称之为Ferrers图，如下图所示。

Ferrers图像具有如下性质：

1.    每一层至少有一个格子。

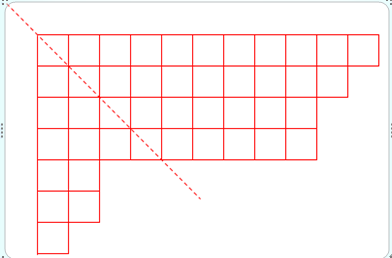
2.    第一行与第一列互换，第二行与第二列互换，……，即上图绕虚线轴旋转所得的图仍然是Ferrers图像。这个的两个Ferers图像称为一对共轭的Ferrers图像。

利用Ferrers图像可以得到整数拆分的非常有趣的结果。

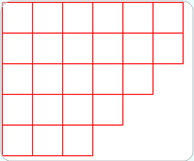
（a） 整数n拆分成k个数的和的拆分数，和数n拆分成最大数为k的拆分数相等。因整数n拆分成k个数的和的拆分可用一k行的图像表示。所得的Ferrers图像的共轭图像最上面一行有k个格子。例如：

            

24=6+6+5+4+3                             

5个数，最大数为6

              

24=5+5+5+4+3+2

6个数，最大数为5

（b） 整数n拆分成最多不超过m个数的和的拆分数，和n拆分成最大不超过m的拆分数相等。 理由与（a）类似。

（c） 整数n拆分成互不相同的若干奇数的和的拆分数，和n拆分成自共轭的Ferrers图像的拆分数相等。

设n=(2n₁+1)+(2n₂+1)+……+2(n_k+1)，其中n₁>n₂>……n_k。

构造一个Ferrers图像，其第一行，第一列都是n1+1格，对应于2n₁+1，第二行，第二列各n₂+1格，对应于2n₂+1。依此类推。由此得到的Ferrrers图像是共轭的。反过来也一样。

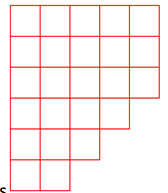
例如：17=9+5+3

对应的Ferrers图像为：