图的强连通分量，块，割点，桥

写在前面：整合和参考了网上的一些相关文章和刘汝付佳的《内功心法》里的部分内部。

      因为在求强连通分量，块，割点，桥的时候，其基本过程是DFS，所以对DFS的一基本的知识作些介绍。

      为了叙述方便，规定DFS过程将给结点着色：白色为没有考虑过的点，黑色为已经完全考虑过的点，灰色为发现过但没有处理过的点。灰色点组成了遍历边界。

DFS遍历

      DFS遍历优先扩展新发现的结点，它的过程可以看作是递归的。算法将得到DFS森林，类似于BFS树。DFS的特别之处在于可以进行边分类。我们首先需要在遍历时加上时间戳(time stamp)。

             发现时间d[u] 结点变灰的时间

             结束时间 f[u]结点变黑的时间

      初始化time为0，所有点为白色，DFS森林为空。则只需要对每个白色点u执行一次DFS-VISIT(u)，每次处理一个点前和处理完后翥把当前时间加1，则所有点u的时间戳满足1<=d[u]&&f[u]<=2|v|。显然其时间复杂度是O(n+m)的。

这里有一个例子：

这里有一个例子：

所有时间戳都不同，且为1到2|V|的整数。从下图还可以直观看到，对于任意结点对(u, v)，区间[d[u], f[u]]和[d[v], f[v]]要么完全分离，要么相互包含。如果u的区间完全包含在v的区间内，则在DFS树中u是v的后代。

      关于DFS树，我们有重要的：

白色路径定理 在DFS森林中v是u的后代当且仅当在u刚刚被发现时，v可以由u出发只经过白色结点到达。定理十分直观，证明略。

  DFS-VISIT可以顺便将边(u, v)分成以下几类：

             树边(Tree edges, T) v通过边(u, v)发现。

             后向边(Back edges, B) u是v的后代。

             前向边(Forward edges, F) v是u的后代。

             交叉边(Cross edges, C)：其他边。可以连接同一个DFS树中没有后代关系的两个结点，也可以连接不同DFS树中的结点。

边分类算法把分类规则落实到程序中，只需要考虑边(u,v)时检查v的颜色：

      v是白色，(u,v)是T边

      v是灰色，(u,v)是B边，因此只有此时u的祖先是灰色

      v是黑色，继续判断。若d[u]<d[v]，说明v是u的后代，因此是F边，否则是C边。否则是C边。

      DFS的时间复杂度仍为O(n+m)。容易证明：无向图只有T边和B边。下面的图把前面的例子中的DFS树画得更加直观，读者可以仔细体会T、B、F、C边是什么样的。

有向图的连通性

      有向图的边都是单向的，因此可达性不具有传递性：u可以到达v，不见得v到达u。但如果u和v相互可达，那么对于任意其他结点w来说，w、u之间的可达性与w、v之间的可达性相同。“相互可达”关系是一个等价关系，因此可以根据这个关系把所有结点分成若干集合，同一个集合内的点相互可达，不同集合内的点不相互可达，如下图：

每一个集合称为有向图的一个强连通分量（Strong Connected Component,SCC）。如果把一个集合看成一个点，那么所有SCC构成了一个SCC图：

求强连通分量的Tarjan算法

      对于每一个强连通分量SCC C，在DFS的过程中，都有一个最早被发现的点，设为x，则由白色路径定理，在C中的其他点都是x的后代。如果我们能在x访问完成时立刻输出C。这样，就可以在一棵DFS树中区分所有SCC了。因此问题的关键就是：判断一个点是否为SCC中最先发现的点。

      如上图，实线表示一条边，虚线表示一条或多条边。假设我们正在判断u是否是某SCC的第一个被发现结点。如果我们从u的儿子出发可以到达u的祖先w，显然u、v、w在同一个SCC中，因此u不是该SCC中第一个被发现的点。如果从v出发最多只能到达u，那么u是该SCC的第一个被发现的结点。这样，问题转化为求：一个点u最远能达到的祖先的d值。注意，这里的“到达”可以通过B边，不能通过C边，但前提是只能通过当前的搜索子树里的有的点（在程序里用栈保存的）而不是其他已经找出来的SCC里的点。

      定义low[u]为u及其后代能追溯到的最早（最先发现）祖先点v的时间戳dfn[v]（dfn[v]表示v变灰的时间，即v最早发现的时间）

      程序用sta栈保存当前SCC中的结点（注意这些结点形成一棵子树，而不一定是一个链）。idx表示时间戳， scnt为SCC计数器，id[i]表示i所在的SCC编号，insta[i]表示i是否在栈中。注意限制v必须在栈中，因为从C边出发可能到达已经输出的SCC中。

vector<int> adj[N];
int low[N],dfn[N],id[N],sta[N],idx,top,scnt;//scnt从1开始
bool insta[N];
void tarjan(int u)
{
	insta[u]=1;	sta[top++]=u;
	low[u]=dfn[u]=++idx;
	for(int i=0;i<(int)adj[u].size();i++) {
		int v=adj[u][i];//用vector存的点
		if(!dfn[v]) {
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(insta[v]&&dfn[v]<low[u]) low[u]=dfn[v];
	}
	if(low[u]==dfn[u]) {
		int tmp;
		++scnt;
		do {
			tmp=sta[--top];
			//vis[tmp]=0;这里写错了。
			insta[tmp]=0;//应该是把在栈中的标记取消。
			id[tmp]=scnt;
		}while(tmp!=u);
	}
}

无向图的连通性

      求无向图的连通分量是平凡的，但无向图的连通性问题远不止于此。如果连通无向图G中存在一个点u，删除u后G不同连通，则称u为G的一个割顶（articulation point）。没有割顶的连通图称为双连通图（Biconnectedgraph）。对于任意两条边e1和e2，如果e1=e2或者它们在同一个环中，则称它们满足关系R。容易证明R是一个等价关系。根据此等价关系我们把G的边分为不相交集E1，E2，…，Ek，设Vi是Ei中包含的点集，则每个子图Gi={Vi,Ei}称为G的一个双连通分量（Biconnected component，BCC）或称块（block）。双连通分量具有如下性质：

      1.    双连通分量都是双连通的。

      2.   任意两个不同的双连通分量最多只有一个公共点。

      3.   结点u是图G的割顶当且仅当是某两个不同的双连通分量的公共点。

      注意到在无向图中只有B边和T边两种，因此DFS可以很方便的求出G的所有双连通分量。首先我们需要判断出所有割顶。关于割顶，我们有以下引理。

引理：对于连通无向图G={V,E}，S={V,T}为G的一个DFS树，则结点u是G的割顶当且仅当下面条件之一被满足：

      1.  u是T的根且u至少有两个儿子

      2.  u不是T的根且存在u的某个儿子w，使得从w或者w的后代没有边连回u的祖先（注意，不是连回u本身）。

证明：首先考虑u是根的情况。如果它有两个儿子v和w，其中v先被发现。由于w不是v的后代，所以v到w没有白色路径。由于v和w是连通的，而且此时只有u被标记为灰，所以v到w的所有点都必须经过u。删除u后v和w不再连通。反过来，如果u只有一个儿子，删除以后显然剩下点在T-{u}中连通，当然在G-{u}中也连通了。

      如果u不是根，情况如下图。如果w或w的后代没有连回u祖先的边，那么w到u父亲f的所有路必须经过u。注意无向图是没有F边和C边的，所以w及后代只能通过B边连回祖先。

       反过来，如果u的每个儿子都可以连回f（如果可以连轴得更远，顺着树边走最终可以到f），删除u至少不会引起u的这些儿子和f不连通。有没有可能引起另外两个点不连通呢？假设存在x和y使得删除u后引起x和y不连通。显然x和y至少有一个应该是u的后代，否则不考虑以u为根的子树x和y也可以通过T的剩下部分连通。这样，设x是u的后代。注意我们假设的是x可以连回f，因此图看起来应该是下面两种情况之一：

      情况一 y不是u的后代，这样x先走到f，再沿着T中的边走到v，并没有经过u。

      情况二 y也是u的后代，则y也可连回f。这样x先走到f，再从f到y，并没有经过u。

      在这两种情况下，都不会引起x和y的不连通。

      类似于割顶，我们可以定义无向连通图的桥(bridge)：如果删除一条边e后无向图G不再连通，称e为G的桥。桥的判定也不难，只需要在发现T边(u,v)时进行判断。如果v后它的后代无法连回u或者u的祖先，则删除(u, v)后u和v不连通。即：发现T边(u, v)并递归遍历v后若dfn[u]<low[v]，则(u, v)为桥。类似于割顶，我们称没有桥的图为边连通图。如果一个无向图是边连通的，可以把它的边定向，得到一个强连通的有向图。

      low[u]、dfn[u]、idx和上一个程序的定义是相同的，fa表示转移到u结点的u的父亲结点，cnt表示当前结点u有个儿子结点，root表示这棵DFS搜索树的根结点。

求割点和桥

void tarjan(int u,int fa)
{
	int cnt=0;
	low[u]=dfn[u]=++idx;
	for(int i=0;i<(int)adj[u].size();i++)
	{
		int v=adj[u][i];
		if(v==fa) continue;
		if(!dfn[v]) 
		{
			tarjan(v,u);
			++cnt;
			low[u]=min(low[u],low[v]);
			if( (root==u&&cnt>1)||(root!=u&&dfn[u]<=low[v]) ) //判断是否是割点
				isap[u]=1;
			if(dfn[u]<low[v]) cutE[++numE]=Edge(u,v);//判断是否是桥,视具体情况采用恰当的结构记录。
		}
		else low[u]=min(low[u],dfn[v]);//这里不用判断是否点v在栈中
	}
}

为什么这个程序不用判断点v是否在栈中呢？

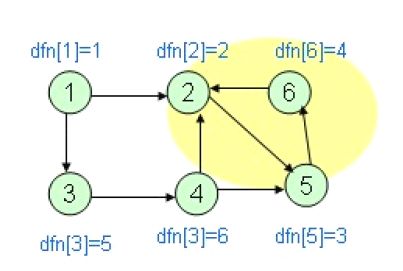
举个例子：

       根据dfn 可以看出搜索的顺序是1->2->5->6形成一个强连通分量(2,5,6)，于是开始退栈,回溯到1 从3 出发到达4,此时如果直接用dfn[2]更新low[4]的话，会得到low[4]=2,变小后而与dfn[4]不再相等，不能退栈，这与最后的4形成一个单独强连通分量是不符合的，所以，不在栈中的点，不能用来更新当前点的low[]值，为什么无向图不用标记呢，那时因为，边是无向的，有边从4->2同时也必有边2->4 由于2 之前被标记过，而遍历到当前结点4 又不是通过w(2,4)这条边过来的，则必还存在另一条路径可以使2 和4 是相通的，(即图中的4-3-1-2),从而2,4 是双连通的。

      无向图的缩点与有向图是类似的，只要把无向图转化成有向图，即对于每条无向边(u,v)，建成有向边u->v，v->u即可。

      当然也有无向图的作法，只是在有向图的基础上变动了一点。

void tarjan(int u,int pre)
{
	sta[top++]=u;
	low[u]=dfn[u]=++idx;
	bool flag=1;
	for(int i=0;i<(int)adj[u].size();i++) {
		int v=adj[u][i];//用vector存的点
		if(v==pre&&flag) //判重边
		{
			flag=0; continue;
		}
		if(!dfn[v]) {
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(dfn[v]<low[u]) low[u]=dfn[v];
		//为什么这里可以不要求[v]在栈中上面解释过了。
	}
	if(low[u]==dfn[u]) {
		int tmp;
		++scnt;
		do {
			tmp=sta[--top];
			id[tmp]=scnt;
		}while(tmp!=u);
	}
}

       在无向图中也可以这么写。前面的写法是规定low[u]是其子孙通过一条返祖边直接到达的点，把这个改成是其子孙可以连续通过多条返祖边所能到达的点。那么low[u]=min(low[v],low[u]);

void tarjan(int u)
{
	sta[top++]=u;
	low[u]=dfn[u]=++idx;
	for(int i=0;i<(int)adj[u].size();i++) {
		int v=adj[u][i];//用vector存的点
		if(!dfn[v]) tarjan(v);
		low[u]=min(low[u],dfn[v]);
		//为什么这里可以不要求[v]在栈中上面解释过了。
	}
}

       这样做的缺陷是，不能求割点了，多次返祖会导致求割点的错误，在多环两两以单个点相连排成一条线，且每两个连接点间只有一条边的情况中，那些连接点本应是割点，但是在dfs过程中，这些连接点之间的边又恰好不是树枝边的话，low[u]可能会通过多次返祖,从一个割点不断的经过这些割点到达最上边的割点才记录下low[u]。

      这样中间的割点就都不符合dfn(u)<=low[v]了。

      但是这样做有一个好处，就是所有的对于边的双连通分支都以low标记出来了，即属于同一双连通分支的所有点的low都等于同一个值。因为在不遇到桥的情况下，low可以返祖到该连同分支在遍历树中的最高点（dfn最小的点）。

求无向图的块

void dfs(int v)  
{  
    low[v]=dfn[v]=++itime;  
    sta[top++]=v;  
    for(int i=head[v];i!=-1;i=edge[i].pre)  
    {  
        int to=edge[i].to;  
        if(dfn[to]) low[v]=min(low[v],dfn[to]);  //因为是无向边，所以没有在不在栈中的限制
        else   
        {  
            dfs(to);  
            low[v]=min(low[v],low[to]);  
            if(dfn[v]<=low[to])  				//如果它的子图里的点都没有办法到达v的祖先节点，说明构成一个连通子图。
            {  
                block.clear();  
                while(1)  
                {  
                    block.push_back(sta[top-1]);  
                    if(sta[--top]==to) break;  //没有把v弹出
                }  
                block.push_back(v);  			//虽然没有弹出，但是也放到统计里。
                count();  
            }  
        }  
    }  
}