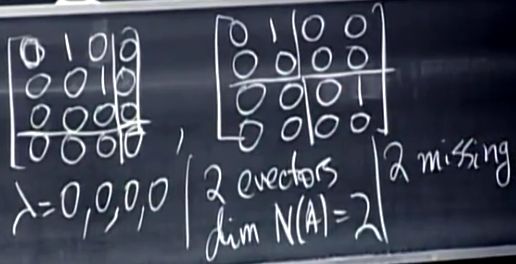线性代数导论29——相似矩阵和若尔当形

本文是Gilbert Strang的线性代数导论课程笔记。课程地址： http://v.163.com/special/opencourse/daishu.html  

第二十九课时：相似矩阵和若尔当形

本讲介绍相似矩阵，两个矩阵相似意味着什么。

正定矩阵

回顾上讲内容，正定矩阵有 x ^T Ax>0 ，也可直接通过特征值，主元或者行列式来做判断。

假设A是一个正定矩阵，它是一个对称矩阵，那么A的逆矩阵也是对称的，而且，A的逆的特征值等于原矩阵特征值的倒数，如果能判断原矩阵是正定的，那么它的逆也能确定是正定的。

如果A,B都是正定矩阵，那么A+B也是正定的。证明：已知 x ^T Ax>0， x ^T Bx>0，那么 x ^T ( A+B)x>0。

实际上大量的物理问题需要用长方形矩阵描述。

正定矩阵从何而来？它来自最小二乘法。最小二乘的关键在于矩阵A^T A，可证明它是一个正定矩阵。

假设有长方矩阵Am×n，那么 A ^T A是对称矩阵。

x ^T( A ^T A ) x = ( Ax) ^T ( Ax) = | Ax| ²  > = 0，当Ax为零向量时等式等于0， Ax=0 ，如何保证A的零空间里只有零向量？

当A各列线性无关，rank(A)=n时，零空间只有零向量。此时，A^TA是正定的，最小二乘方程将存在最优解。

正定性把以前的内容都串联起来。现在要进入线性代数最核心的内容了。

相似矩阵

A和B是两个n×n方阵，如果存在某个可逆矩阵M，使得：B=M^-1 AM，那么A和B是相似的。

其中任意两个互为相似的矩阵满足上述等式。

假设A有无关的特征向量，通过特征向量矩阵S，有： S^-1AS=Λ，那么A相似于 Λ。对角阵是这类矩阵（互为相似矩阵）中最与众不同的。它是这类矩阵里面最简洁的一个。矩阵A的所有相似矩阵里面， Λ是最好的，还有许多其他矩阵与A相似。我们可以用任意的可逆矩阵M代替S,都得到一个新的矩阵，这个新的矩阵与A相似。那么A与其他所有的相似矩阵的共同点是什么？

性质1）相似矩阵具有相同的特征值；（注意特征向量并不相同）

具有相同特征值的一类矩阵，两个矩阵之间由一个可逆M联系起来，这类矩阵里面最特殊的就是对角阵 Λ。为什么 相似矩阵具有相同的特征值？

有Ax=λx，假设λ是A的特征值，那么A M M ^-1 x =λx，等式两边同时乘以 M ^-1 ， M ^-1A M M ^-1 x =λ M ^-1x，同时有 B=M ^-1 AM，所以前面的式子化为：B M ^-1 x  =λ M ^-1x，此等式表明λ是B的一个特征值。由此也可得性质2.

性质2）B=M^-1AM， B的特征向量等于M的逆乘以矩阵A的特征向量；

对角阵Λ是A的最简单特殊的相似矩阵， Λ的特征向量为(1 0),(0 1)。

有一种坏情况

当矩阵A有重复的特征值，那么意味着A的特征向量会共线，矩阵可能无法对角化。

假设A的特征值： λ1=λ2=4，A=([4 0],[0 4])，那么M^-1 AM仍旧为A，这样的对角矩阵是单一的一类矩阵，它的相似矩阵只有自己。

另一种情况，如上，下部分，λ1=λ2=4，这是一个无法对角化的矩阵，它可以找到一类矩阵与它相似，如果把右上角的元素换成10或者其他的数，也是一样的能找到相应的M使之与其相似，但右上角是1的特征值重复的三角矩阵称为 若尔当标准型Jordan form。 若尔当标准型是最接近对角阵的一个，但又不完全对角化。

对于之前无法对角化的矩阵，都可以通过某种特殊方法，完成近似的“对角化”。如果想要对角化任何矩阵，则必须学习这种方法。

另一类相似矩阵：他们的迹和行列式相等。比如下面的，他们的特征值相等，且所有的特征值都是重复的。

另一类矩阵，若尔当认为它们并不是相似的。

如下第一个矩阵，λ1=λ2=λ3=λ4=0，特征向量为整个零空间，零空间是二维的。如果把第一行的第三个元素改为7，特征值仍然相等，特征向量个数仍然相等，修改过的矩阵和原先的矩阵相似，但因为之前的矩阵很美观，所以选择前者。注意对角线上的1，每增加一个1，特征向量就减少1个。

第二个矩阵,4个特征值仍然全为0，特征向量的个数为2，但若尔当认为第二个矩阵并不相似与第一个矩阵。第一个矩阵由3×3的矩阵和1×1的矩阵若尔当块组成，第二个矩阵由两个2×2的分块组成，这些分块称为若尔当块。 因为若尔当块大小不一样，所以若尔当认为两个矩阵并不相似。

  

若尔当块：Ji表示i阶的若尔当块，它只有一个重复的特征值，对角线上全是λi，下面是0，上面是1，它的对角线上都是同一个数，只有一个特征向量。即，每个若尔当块只有一个特征向量。

若尔当阵J：由若尔当块构成的矩阵，特征值位于对角线上，对角线上方有若干个1，若尔当块的数量等于特征向量的个数，因为每一块对应于一个特征向量。

若尔当定理：每个方阵A都相似于一个若尔当阵J。如果方阵A有n个互不相同的特征值，那么它是一个可对角化的矩阵，对应的若尔当阵就是对角阵Λ，J=Λ，d=n 。

若尔当研究了所有情况，包含特征值重复的情况，此时特征向量的个数变少，这就是若尔当的理论。