机器学习实战——组合方法与AdaBoost
对于分类问题,在给定数据集前提下,训练比较粗糙的弱分类器比精确的强分类器容易得多。另外,Schapire证明了强可学习与弱可学习是等价的,因此首先学习简单的弱分类器,并进行组合就可以得到强分类器,这就是组合方法的理论基础。
组合(Ensemble)方法是一种提高分类准确率的方法,是一个由多个弱分类器组合的复合模型,其中每个单个分类器都进行投票,组合分类器返回最终组合的结果,这样分类的结果比单个分类器的结果更准确。
组合分类常见的方式有bagging(套袋)、boosting(提升)、random forest(随机森林)。这些方法使用给定的数据集 D 使用不同的方法创建 k 个训练集 D1,D2...Dk ,对每一个数据集 Di 使用确定的方法创建一个分类器 Mi ,最终组合分类器将学习到的 k 个模型使用不同的方式组合在一起,创建一个复合模型。通过上面的描述,可以发现,组合分类方法的关键点如下:
1. 生成 k 个训练集的方法
2. 每个分类器的训练算法
3. 组合 k 分类器的方式
bagging使用有放回抽样的方式,从训练集中抽取 N 次,形成一个和源数据大小相同的数据集,这样重复进行 k 轮,就可以得到 k 个训练集。由于是有放回抽样,因此原始数据集中有些样本可能不会出现在 Di 中,而有些样本可能出现很多次,一个样本被抽取作为训练集的概率为 1N ,因此不被抽中的为 1−1N ,抽取 N 次都不能被抽中的概率为:
random forest也是使用上述有放回抽样的方式得到训练集,但是在每个分类器训练时采用的是构建决策树,使用CART算法进行增长,随机选择给定个属性进行构建,不进行剪枝,称为Forest-RI。还有另外一种形式是对输入属性进行随机线性组合,产生多个线性组合找到最佳划分从而构建决策树。最终进行分类时每一课决策树都进行投票,返回得票数最多的类别。
boosting方法则是对每个训练的样本赋予一个权重,通过每次训练改变每个样本的权重(也就是训练数据的 概率分布)得到新的训练集,没有前面所述的有放回抽样得到 k 训练集的过程,只是进行改变权重的过程进行迭代学习 k 次,相当于是得到了 k 个训练集和分类器,每个分类器 Mi 更新权重之后,将其错分类的样本赋予更高的权重,使得 Mi+1 分类器更加关注错分的样本。最终 组合的分类器是每个分类器的加权结果,这个权重是相应分类器分类的准确率的函数。不同于bagging的组合方式中每个分类器是一样的权重进行投票的。
本文重点关注的是使用最广泛也是被很多人称为最好的监督学习方法——AdaBoost方法,这是一种最流行的boosting方法。
AdaBoost策略
给定训练数据 D={(X1,Y1),(X2,Y2),...(XN,YN)} , Yj∈{+1,−1} 属于二分类问题。初始条件下,赋予每个样本 (Xj,Yj) 相等的权重 w(j)i=1N (下标为训练的轮数,上标为样本标号),也就是数据是均匀分布的。
1. 每一轮如何改变训练数据的权值(概率分布)
第 i 轮训练中,得到分类器 Mi ,使用该分类器计算错误率 erri :
然后对每个样本,更新权重为 wi+1 :
2. 如何将弱分类器组合成强分类器
根据上述计算,得到了第 i 轮训练时的分类器权重 αi ,因此最终构建分类器的加权和:
这就将 k 个弱分类器组合得到了最终的强分类器,而且权重 αi 是与对应的分类器错误率相关的,如果错误率 erri 越小,则 αi=12log1−errierri 越大,从而在最终的强分类器中的权重越大。这就正好对应了,错误率小的分类器对最终分类结果的决定性作用更大。
AdaBoost模型解释
AdaBoost是模型为加法模型,学习策略为指数损失函数的经验风险最小化,学习算法为前向分步算法的二分类方法。
加法模型是从前往后,每一轮仅学习一个模型及其系4数,这样逐步逼近最终目标。也就是对应AdaBoost中,每一轮学习一个弱分类器,通过错误率再计算权重 αi 。记第 i−1 轮学习到的模型组合为 fi−1 :
那么得到:
对于上述目标函数,最优的分类器由如下确定:
对于权重 αi 有
上述目标对 α 求导并使导数为0即可得到最优的 α∗i :
AdaBoost算法实践
根据上述算法,使用之前的垃圾邮件分类数据进行分类,每个分类器构建的都是一个单节点的决策树,也就是一个树桩,在训练数据集中找出加权错误率最小的一个分割点,然后按照上述方法进行分类器权重计算和每个样本的权值更新。
分割点的查找
对数据的每个维度,都要进行查找,在给定维度下,找到最大和最小的数据,每次以给定步骤进行查找,计算错误率,最终找到最佳分割点。具体实现如下:
def findSpliter(ds, labels, weight):
'''find the best spliter for min error rate'''
spliter = {'featIndex': 0, 'thresh': 0, 'cmp': 'le', 'minErr': inf}
cls = None
m,n = ds.shape
steps = 20.0
index = range(n); #random.shuffle(index)
for i in index:
rangeMin = ds[:, i].min(); rangeMax = ds[:, i].max()
step = (rangeMax - rangeMin) / steps
for j in range(-1, int(steps) + 1):
for comp in ['le', 'gt']:
thresh = rangeMin + float(j) * step
splitCls = spliterClassify(ds, i, thresh, comp)
err_i = mat(ones((m, 1)))
err_i[labels == splitCls] = 0
err_rate = sum(err_i.transpose() * weight)
if err_rate < spliter['minErr']:
spliter['minErr'] = err_rate
spliter['featIndex'] = i
spliter['thresh'] = thresh
spliter['cmp'] = comp
cls = splitCls.copy()
return spliter, cls训练
模型的训练过程就是在给定分类器个数的条件下,每轮寻找最佳分割点构建单节点决策树,同时计算权重 alphai 和样本分布 w ,并进行更新,最后计算出所有基本分类器和权重。
def AdaBoostTrain(ds, labels, maxSteps=200):
weakClassfier = []
alpha = []
savedWeight = []
m,n = ds.shape
weight = mat(zeros((m, 1)))
weight[:,:] = 1.0 / m #initial weight
for i in range(maxSteps):
savedWeight.append(weight)
spliter, cls = findSpliter(ds, labels, weight)
err = spliter['minErr']
alpha_i = 0.5 * log((1 - err) / err)
alpha.append(alpha_i)
weakClassfier.append(spliter)
#update weight
aiYiMi = multiply(-1.0 * alpha_i * labels, cls)
Z = multiply(exp(aiYiMi), weight)
weight = Z / Z.sum()
return weakClassfier, alpha, savedWeight分类
分类过程就是将训练好的模型对待分类数据进行分类,然后使用训练得到的权重进行加权组合分类结果,最终得到的分类结果由加权组合结果取符号函数得到。实现如下:
def AdaBoostClassify(weak, alpha, ds):
classes = []
for i in range(len(alpha)):
splitCls = spliterClassify(ds, weak[i]['featIndex'], weak[i]['thresh'], weak[i]['cmp'])
cls = splitCls * alpha[i]
classes.append(cls)
predicted = reduce(lambda x,y: x+y, classes)
predicted[predicted >= 0] = 1
predicted[predicted < 0] = -1
return predicted分类结果
对垃圾邮件数据进行实际训练和分类,最终得到了训练集和测试集的错误率,并绘制了结果图如下所示:
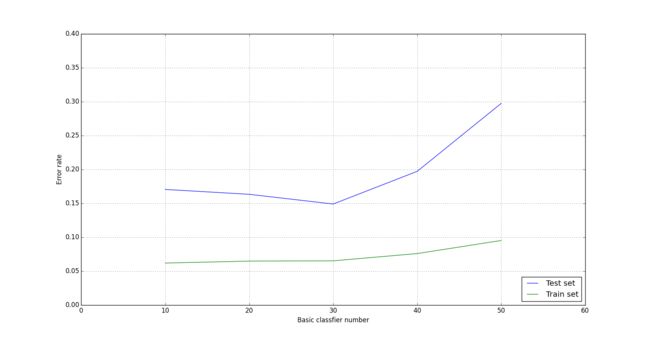
从图中可以看出,随着基本分类器个数的增加,测试集错误率先减小,得到最小错误率后逐步增大,这正是欠拟合和过拟合的表现,最终需要选择分类器个数为30时的泛化误差最小。