杭电OJ(HDOJ)2036题:改革春风吹满地(几何,数学公式)
题意:
输入数据包含多个测试实例,每个测试实例占一行,每行的开始是一个整数n(3<=n<=100),它表示多边形的边数(当然也是顶点数),然后是按照逆时针顺序给出的n个顶点的坐标(x1, y1, x2, y2... xn, yn),为了简化问题,这里的所有坐标都用整数表示。输入数据中所有的整数都在32位整数范围内,n=0表示数据的结束,不做处理。对于每个测试实例,请输出对应的多边形面积,结果精确到小数点后一位小数。每个实例的输出占一行。
示例输入:
3 0 0 1 0 0 1
4 1 0 0 1 -1 0 0 -1
0
示例输出:
0.5
2.0
错误解决方案:
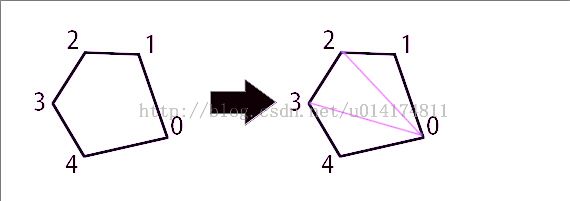
按逆时针给出若干个顶点的坐标,设有5个顶点,得出以下多边形:
从顶点0出发,有两条线将其分成了(0,1,2)(0,2,3)(0,3,4)三个三角形,只要求出这个三个三角形的面积和就是这个多边形的面积。已知三个顶点求这个这角形的面积用海伦公式:s=sqrt(p*(p-a)*(p-b)*(p-c)),p=(a+b+c)/2。
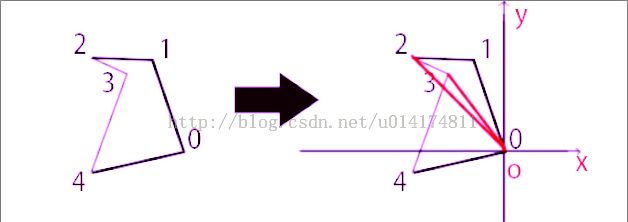
那个问题来了,要是下面这种点是凹进去的,怎么办?
那么看下正确的解决方案。
#include<stdio.h>
#include<math.h>
typedef struct point
{
double x;
double y;
}Point;
double Area(int a,int b,int c,Point p[100])
{
double aa,bb,cc,pp;
aa=sqrt((p[a].x-p[b].x)*(p[a].x-p[b].x)+(p[a].y-p[b].y)*(p[a].y-p[b].y));
bb=sqrt((p[b].x-p[c].x)*(p[b].x-p[c].x)+(p[b].y-p[c].y)*(p[b].y-p[c].y));
cc=sqrt((p[c].x-p[a].x)*(p[c].x-p[a].x)+(p[c].y-p[a].y)*(p[c].y-p[a].y));
pp=(aa+bb+cc)/2.0;
return sqrt(pp*(pp-aa)*(pp-bb)*(pp-cc));
}
int main()
{
Point p[100];
int n,i;
double areaSum;
while(scanf("%d",&n)&&n)
{
areaSum=0;
for(i=0;i<n;i++)
scanf("%lf%lf",&p[i].x,&p[i].y);
for(i=2;i<n;i++)
{
areaSum+=Area(0,i-1,i,p);
}
printf("%.1lf\n",areaSum);
}
}
正确解决方案:
#include<stdio.h>
#include<math.h>
typedef struct point
{
double x;
double y;
}Point;
int main()
{
Point p[100];
int n,i;
double areaSum;
while(scanf("%d",&n)&&n)
{
areaSum=0;
for(i=0;i<n;i++)
scanf("%lf%lf",&p[i].x,&p[i].y);
for(i=1;i<n;i++)
{
areaSum+=(p[i-1].x*p[i].y-p[i].x*p[i-1].y)/2.0;//交叉相乘
}
areaSum+=(p[n-1].x*p[0].y-p[0].x*p[n-1].y)/2.0;//首尾交叉相乘
printf("%.1lf\n",areaSum);
}
}