统计相关系数(3)——Kendall Rank(肯德尔等级)相关系数及MATLAB实现

Kendall Rank（肯德尔等级）相关系数

1、简介

在统计学中，肯德尔相关系数是以Maurice Kendall命名的，并经常用希腊字母τ（tau）表示其值。肯德尔相关系数是一个用来测量两个随机变量相关性的统计值。一个肯德尔检验是一个无参数假设检验，它使用计算而得的相关系数去检验两个随机变量的统计依赖性。肯德尔相关系数的取值范围在-1到1之间，当τ为1时，表示两个随机变量拥有一致的等级相关性；当τ为-1时，表示两个随机变量拥有完全相反的等级相关性；当τ为0时，表示两个随机变量是相互独立的。

 

假设两个随机变量分别为X、Y（也可以看做两个集合），它们的元素个数均为N，两个随即变量取的第i（1<=i<=N）个值分别用X_i、Y_i表示。X与Y中的对应元素组成一个元素对集合XY，其包含的元素为(X_i, Y_i)（1<=i<=N）。当集合XY中任意两个元素(X_i, Y_i)与(X_j, Y_j)的排行相同时（也就是说当出现情况1或2时；情况1：X_i>X_j且Y_i>Y_j，情况2：X_i<X_j且Y_i<Y_j），这两个元素就被认为是一致的。当出现情况3或4时（情况3：X_i>X_j且Y_i<Y_j，情况4：X_i<X_j且Y_i>Y_j），这两个元素被认为是不一致的。当出现情况5或6时（情况5：X_i=X_j，情况6：Y_i=Y_j），这两个元素既不是一致的也不是不一致的。

 

这里有三个公式计算肯德尔相关系数的值

 

公式一：

其中C表示XY中拥有一致性的元素对数（两个元素为一对）；D表示XY中拥有不一致性的元素对数。

注意：这一公式仅适用于集合X与Y中均不存在相同元素的情况（集合中各个元素唯一）。

 

公式二：

注意：这一公式适用于集合X或Y中存在相同元素的情况（当然，如果X或Y中均不存在相同的元素时，公式二便等同于公式一）。

其中C、D与公式一中相同；

；；

N1、N2分别是针对集合X、Y计算的，现在以计算N1为例，给出N1的由来（N2的计算可以类推）：

将X中的相同元素分别组合成小集合，s表示集合X中拥有的小集合数（例如X包含元素：1 2 3 4 3 3 2，那么这里得到的s则为2，因为只有2、3有相同元素），U_i表示第i个小集合所包含的元素数。N2在集合Y的基础上计算而得。

 

公式三：

注意：这一公式中没有再考虑集合X、或Y中存在相同元素给最后的统计值带来的影响。公式三的这一计算形式仅适用于用表格表示的随机变量X、Y之间相关系数的计算（下面将会介绍）。

参数M稍后会做介绍。

 

以上都是围绕用集合表示的随机变量而计算肯德尔相关系数的，下面所讲的则是围绕用表格表示的随机变量而计算肯德尔相关系数的。

 

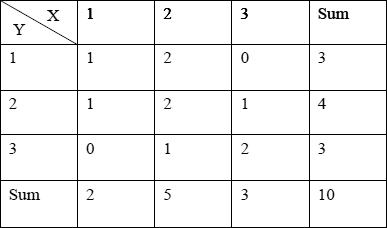
通常人们会将两个随机变量的取值制作成一个表格，例如有10个样本，对每个样本进行两项指标测试X、Y（指标X、Y的取值均为1到3）。根据样本的X、Y指标取值，得到以下二维表格（表1）：

由表1可以得到X及Y的可以以集合的形式表示为：

X={1, 1, 2, 2, 2, 2, 2, 3, 3, 3}；

Y={1, 2, 1, 1, 2, 2, 3, 2, 3, 3}；

得到X、Y的集合形式后就可以使用以上的公式一或公式二计算X、Y的肯德尔相关系数了（注意公式一、二的适用条件）。

当然如果给定X、Y的集合形式，那么也是很容易得到它们的表格形式的。

 

这里需要注意的是：公式二也可以用来计算表格形式表示的二维变量的肯德尔相关系数，不过它一般用来计算由正方形表格表示的二维变量的肯德尔相关系数，公式三则只是用来计算由长方形表格表示的二维变量的Kendall相关系数。这里给出公式三中字母M的含义，M表示长方形表格中行数与列数中较小的一个。表1的行数及列数均为三。

 

2、适用范围 

肯德尔相关系数与斯皮尔曼相关系数对数据条件的要求相同，可参见统计相关系数(2)--Spearman Rank(斯皮尔曼等级)相关系数及MATLAB实现中介绍的斯皮尔曼相关系数对数据条件的要求。

 

3、Matlab实现

源程序一：

肯德尔相关系数的Matlab实现（依据公式二得到）

function coeff = myKendall(X , Y) % 本函数用于实现肯德尔等级相关系数的计算操作 % % 输入： % X：输入的数值序列 % Y：输入的数值序列 % % 输出： % coeff：两个输入数值序列X，Y的相关系数 if length(X) ~= length(Y) error('两个数值数列的维数不相等'); return; end %将X变为行序列（如果X已经是行序列则不作任何变化） if size(X , 1) ~= 1 X = X'; end %将Y变为行序列（如果Y已经是行序列则不作任何变化） if size(Y , 1) ~= 1 Y = Y'; end N = length(X); %得到序列的长度 XY = [X ; Y]; %得到合并序列 C = 0; %一致性的数组对数 D = 0; %不一致性的数组对数 N1 = 0; %集合X中相同元素总的组合对数 N2 = 0; %集合Y中相同元素总的组合对数 N3 = 0; %合并序列XY的总对数 XPair = ones(1 , N); %集合X中由相同元素组成的各个子集的元素数 YPair = ones(1 , N); %集合Y中由相同元素组成的各个子集的元素数 cont = 0; %用于计数 %计算C与D for i = 1 : N - 1 for j = i + 1 : N if abs(sum(XY(: , i) ~= XY(: , j))) == 2 switch abs(sum(XY(: , i) > XY(: , j))) case 0 C = C + 1; case 1 D = D + 1; case 2 C = C + 1; end end end end %计算XPair中各个元素的值 while length(X) ~= 0 cont = cont + 1; index = find(X == X(1)); XPair(cont) = length(index); X(index) = []; end %计算YPair中各个元素的值 cont = 0; while length(Y) ~= 0 cont = cont + 1; index = find(Y == Y(1)); YPair(cont) = length(index); Y(index) = []; end %计算N1、N2及N3的值 N1 = sum(0.5 * (XPair .* (XPair - 1))); N2 = sum(0.5 * (YPair .* (YPair - 1))); N3 = 0.5 * N * (N - 1); coeff = (C - D) / sqrt((N3 - N1) * (N3 - N2)); end %函数myKendall结束

 

源程序二：

使用Matlab中已有的函数计算肯德尔相关系数

coeff = corr(X , Y , 'type' , 'Kendall');

注意：使用Matlab自带函数计算肯德尔相关系数时，需要保证X、Y均为列向量；Matlab自带的函数是通过公式二计算序列的肯德尔相关系数的。

 

这里还有另外一种不是计算肯德尔相关系数的公式（仅适用于集合X与Y中均不存在相同元素的情况，实际上其与公式一等价），可见参考文献(3)。

 

4、参考内容

(1)、http://en.wikipedia.org/wiki/Kendall_tau_rank_correlation_coefficient

(2)、http://www.unesco.org/webworld/idams/advguide/Chapt4_2.htm

(3)、http://www.wikidoc.org/index.php/Kendall_tau_rank_correlation_coefficient