[置顶] “上帝的算法”在高斯混合分布中的应用
吴军老师在《数学之美》中称期望最大值化算法为“上帝的算法”,下面就讨论EM算法在高斯混合分布中的应用。
接高斯判别分析与高斯混合分布之庖丁解牛(第一集)最后剩下的问题继续讨论,以下先不谈什么隐含因子,只是单纯的数学演算,过程非常有意思!
以下的讨论会用到几点知识,我们先作为补充知识,说一下:
补充知识点一:凹函数的定义:
设![]() 是定义在
是定义在![]() 上的函数,若对任意的
上的函数,若对任意的![]() 和任意的
和任意的![]() ,如果满足以下条件,
,如果满足以下条件,
![]() ,
,
则称函数![]() 在
在![]() 上是凹函数。
上是凹函数。
补充知识点二:若函数![]() 的二阶导数
的二阶导数![]() 在
在![]() 上满足
上满足![]() ,则函数是凹函数。显然
,则函数是凹函数。显然![]() 就是凹函数。
就是凹函数。
补充知识点三:jensen不等式:
___________________________________________________________________________________________
设数据集
![]()
是以下高斯混合分布的样本点:
我们接着给出该模型的似然函数的对数:
下面就是对上面对数似然函数的变形,然后引出高斯混合分布:
我们只是同乘以一个![]() ,接着又除以一个
,接着又除以一个![]() ,所以等号成立,其中对任意的
,所以等号成立,其中对任意的![]() ,
,![]() ,
,![]() 满足以下条件:
满足以下条件:
(注意:因为![]() 在分母上,我们暂时先考虑
在分母上,我们暂时先考虑![]() 的情况。后面引出EM算法时,我们会去掉分母上的
的情况。后面引出EM算法时,我们会去掉分母上的![]() 。还有演算到这一步,我们发现这个最优化问题,理论上可以通过梯度下降,kuhn-tucker条件等算法求解,但是太困难,这便是EM算法提出的动机)
。还有演算到这一步,我们发现这个最优化问题,理论上可以通过梯度下降,kuhn-tucker条件等算法求解,但是太困难,这便是EM算法提出的动机)
根据补充知识点二,得出log(x)是凹函数,然后再根据补充知识点三jensen不等式,我们便得到:
更有意思的是,当(下面的公式会很眼熟,就是EM算法的E步)
时,等号成立。
E步,推出来了,那么M步就好做了,我不再仔细推了,直接给出M步:
注意:在这一步,我们就把分母上的![]() 去掉了。为什么去掉,还有为什么收敛,我就不啰嗦了!迭代步骤示意图:
去掉了。为什么去掉,还有为什么收敛,我就不啰嗦了!迭代步骤示意图:
以上便是“上帝的算法”
————————————————————————————————————————————————————————————————————————————
学习EM算法参考资料:
1.【book】:Pattern Recognition and Machine Learning 第九章,这一章还讨论为什么k-均值聚类算法也是EM算法特例
2.Andrew Ng老师的讲义,及公开课视频教程

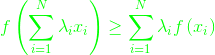




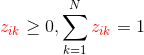
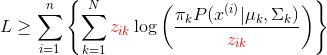


![[置顶] “上帝的算法”在高斯混合分布中的应用_第1张图片](http://img.e-com-net.com/image/info5/32864fa0f14b422494ba6afc6dec8f1e.jpg)