数学黑洞(一)令人拍案叫绝的卡布列克常数
卡布列克是一位数学家,他在研究数字时发现:任意一个不是有完全相同数字的组成的四位数,如果对它们的每位数字重新排序,组成一个最大的数各一个最小的数,然后用最大数减去最小数,差不够四位数时补零,类推下去,最后将变成一个固定的数:6174,这就是卡布列克常数。例如:4321-1234=3087 8730-378=8352 8532-2358=6174 7641-1467=6174。
验证卡布列克运算,任意一个四位数,只要它们各个位上的数字是不全相同的,就有这样的规律:
(1)将组成该四位数的四个数字由大到小排列,形成由这四个数字构成的最大的四位数;
(2)将组成该四位数的四个数字由小到大排列,形成由这四个数字构成的最小的四位数(如果四个数中含有0,则得到的数不足四位);
(3)求两个数的差,得到一个新的四位数(高位零保留)。
重复以上过程(最多7步),最后得到的结果是6174,这个数被称为卡布列克常数。
所以6174也被叫做黑洞数,因为这种现象类似黑洞(进去后就出不来了),也叫“6174问题”,上述变换称为卡普耶卡变换,简称 K 变换。
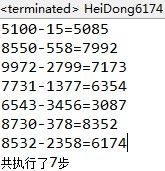
下面我们用程序来验证这个不可思议的事实:
public class HeiDong6174 {
public static void main(String[] args){
helper(1050,0);
}
private static void helper(int num, int count) {
if(num == 6174){
System.out.println("共执行了" + count + "步");
return;
}
String s = String.valueOf(num);
char[] cs = s.toCharArray();
if(cs.length != 4){
System.out.println("请输入一个三位数或者四位数");
return;
}
for(int i = 0; i < cs.length; i++){
for(int j = i; j < cs.length; j++){
if(cs[i] < cs[j]){
char temp = cs[i];
cs[i] = cs[j];
cs[j] = temp;
}
}
}
char[] cs2 = new char[cs.length];
for(int i = 0; i < cs.length; i++){
cs2[i] = cs[cs.length-1-i];
}
int n1 = Integer.parseInt(new String(cs));
int n2 = Integer.parseInt(new String(cs2));
int new_num = n1 - n2;
System.out.println(n1 + "-" + n2 + "=" + new_num);
if(new_num / 1000 < 1)//如果不足四位数,高位补0,等价于低位补0
new_num *= 10;
helper(new_num,count+1);
}
}
测试结果:
6174是卡布列克常数的代名词,还有其他位数的情况:
三位数也有一数495,任何三位数经过这样的运算都会对应到495。其它位数就没有像三位数及四位数这样单纯的状况,会对应到不只一种结果,或是进入数字循环(即数个数循环对应)
5位数的状况:没有黑洞,有3个循环
- 71973 83952 74943 62964 71973
- 82962 75933 63954 61974 82962
- 53955 59994 53955
6位数的状况:有2个黑洞631764、549945,还有1个7个成员的循环
- 420876 851742 750843 840852 860832 862632 642654 420876
7位数的状况:没有黑洞,只有1个8成员的循环
- 7509843 9529641 8719722 8649432 7519743 8429652 7619733 8439522 7509843
8位数的状况:有2个黑洞63317664、97508421
9位数的状况:有2个黑洞554999445、864197532
10位数的状况:有3个黑洞6333176664、9753086421、9975084201
证明如下:转自中国地质大学江城学院邬金华副教授的文章编辑本义项
4位黑洞数的证明及相关问题剖析
自原苏联人卡普耶卡提出4位数反复重排求差会得到黑洞数6174至今,这种看似简单的数字游戏隐含的数学道理已逐渐引起越来越多的人的兴趣,并很快被推演到更多位的情形。网上有消息称,该问题已被“印度学者”和台湾中学生李光宇各自解决,大陆人王景之稍后也在网上公布了他的研究结论,但是,在可以搜索到的材料中却一直没有见到有关的严格的数学证明,而且,台湾李光宇和大陆王景之的结论也不完全一致。为弥补这些缺憾,这里先介绍几种对经典4位黑洞数的证明方法和相关结论,随后再陆续公布对其它位数的研究结果。
一、操作过程中的差数
在反复重排求差的演算过程中,除首次演算时的被减数是某个任意4位数(但4个数字不全相同)以外,以后操作的被减数都是上一次差数的重排,就是说,以后的操作都是在差数基础上进行的,而且黑洞数本身也是一个差数,只是较为特殊罢了。为了揭示一般差数的特点,这里将重排求差时的最大数用大写字母ABCD的形式写出(最小数随之而定),差数用小写字母mnpk的形式写出。按最大数中间二位数字是否相同,可将最大数和相应得到的差数分为两种类型。
类型1:最大数中间二位数字不同,即A≥B>C≥D,称无核类型(0核类型),或普通类型。
将相减操作写成竖式,可以得到被减数、减数和差数各构成数字之间的基本关系式:
m=A-D m+k=10
n=B-C-1 n+p=8
p=C-B+9 m>n
k=D-A+10
很明显,所有差数的共同特点是:首尾二数字之和必为10,中间二数字之和必为8,首位数大于二位数。这样,能作为差数出现的数并不多,这里将它们从小到大全部罗列如下,共1+2+3+……+9=45个:
1089
2085 2178
3087 3177 3267
4086 4176 4266 4356
5085 5175 5265 5355 5445
6084 6174 6264 6354 6444 6534
7083 7173 7263 7353 7443 7533 7623
8082 8172 8262 8352 8442 8532 8622 8712
9081 9171 9261 9351 9441 9531 9621 9711 9801
类型2:最大数中间二位数字相同,即A≥B=C≥D(不能同时都取等号),称有核类型。
同样写成竖式,可得被减数、减数和差数各构成数字之间的基本关系式为:
m=A-D-1 m<9
k=D-A+10 m+k=9
此时差数的首尾二数字之和必为9,但首位数字不能为9,中间二数字永远是99。这类差数只有9个,它们是
0999 1998 2997 3996 4995 5994 6993 7992 8991
综合两种类型,在4位数中,能作为差数出现的数共有54个,他们就是研究4位黑洞数的根本出发点。
二、黑洞数6174的证明
按黑洞数的定义,如果将黑洞数本身也重排求差,那么差数的构成数字就应该与黑洞数的构成数字相同,这样,就可以有3种不同的方法证明黑洞数6174。
证明1——顺推
对上述54个差数逐一重排求差,如果差数的构成数字与被减数的构成数字相同(排列次序可以不同),那么该差数就一定是黑洞数;如果不存在这样的差数,就没有单一的黑洞数。实际上,在54个差数中,大多数差数都可以找到与自己构成数字完全相同的“同伴”,如1089、9081、9801等等,它们都是交换了m、k或n、p位置的结果,它们重排求差时的最大数都是一样的,故可将它们归并为一组,称等效差数数组,简称等效数组。因为有限定条件(m>n或m<9),同一数组中包含的差数的个数可以是1个、2个、3个……,最多可有比位数少1个,这里不妨将他们分别称为一元数组、二元数组、三元数组等等。这里是4位数,最多可包含3个差数,故可归并出一元数组、二元数组和三元数组,共29组。这样,只需针对这29组差数重排求差就可以证明有无黑洞数了。结果,只有数组4176-6174重排求差得6174,其构成数字与最大数7641相同,所以6174就是黑洞数,而且是唯一的。
这里介绍一个求差小窍门,可以很快得到对某数重排求差结果:某数如为类型1的数,其中最大和最小两数字之差即为差数的首位数,剩下两数之差再减1就是差数的二位数,差数的第3位和第4位只需使其与首二位数之和分别为8和10就行了。如对4176或1089重排求差,看下图:
最大减最小得差数的首位
4 1 7 6 6 1 7 4
剩下二数之差再减1得差数的第二位 和为8
和为10
最大减最小得差数的首位
1 0 8 9 9 6 2 1
剩下二数之差再减1得差数的第二位 和为8
和为10
如某数是类型2的数,可用某数中的最大数减最小数再减1作为差数的首位数,差数的中间二数永远是“99”,差数的末位数与首位数之和为9。看下图:
最大减最小再减1得差数的首位
7 4 4 3 3 9 9 6
和为9
证明2——解方程
在前述类型1的基本关系式中,如果最大数ABCD是由黑洞数重排得到,那么差数mnpk应该仍是黑洞数,它的4个构成数字就应该与A、B、C、D分别相同,这样的可能共有4!=24种,但考虑到k≠D,n≠A,p≠C,还有12种,将它们分别代入到基本关系式中就可得到12个四元一次方程组,分别求解(看似麻烦,其实很简单,因为未知数系数都是1,且都是1位数),结果发现,只有m、n、p、k顺序等于B、D、A、C时,方程组才有合乎条件(A≥B>C≥D,且都是1位正整数)的解,解得A=7,B=6,C=4,D=1,或m=6,n=1,p=7,k=4。
对类型2的数可用相同方法处理,但简单分析就知无解。故6174是唯一的黑洞数。
证明3——逆推
这在下面的叙述中将被提到。
三、逆推
所谓逆推,就是指求差的逆运算,即由差数mnpk反推求差时的最大数ABCD。
在类型1中,当mnpk已知时,将m、n、p、k分别代入到基本关系式中,可得4个等式,好像还是解四元一次方程组的问题,但因为已知的mnpk本身就有m+k=10,n+p=8的关系,故4个等式中只有2个是有效的,所以这时的四元一次方程组就成了不定方程;另一方面,ABCD还需满足A≥B>C≥D,故方程组只有有限个解。类型2的情形与此类似,因为已知的m、k已经满足m+k=9,故2个等式中只有1个是有效的,而ABBD也要满足A≥B≥D(不同时取等号),所以方程组也只有有限个解。解这2类不定方程组,可分别得到它们的逆推求解公式。
1、类型1的逆推求解公式
当4位数mnpk满足条件m>n,m+k=10,n+p=8时,可用以下公式逆推求ABCD:
A = m+α (α = 0,1,2……9-m)
B = n+1+β (β =α,α+1,α+2,……α+m-n-1)
C = β
D = α
α、β的取值法则是先使α从0开始一直取到9-m时为止(A和D由此而定),在同一α条件下β可能可取多个值,即从α一直取到α+m-n-1时为止。以黑洞数6174为例,此时m=6,n=1,为清楚起见,可将α、β的取值和相应得到的ABCD列成式子和数表:
A = m+α = 6 +α = 6 6 6 6 6 7 7 7 7 7 8 8 8 8 8 9 9 9 9 9
B = n+1+β =2 +β = 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 5 6 7 8 9
C = β = 0 1 2 3 4 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7
D = α = 0 0 0 0 0 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3
将它们写成正规数的形式就是
6200 6310 6420 6530 6640 7311 7421 7531 7641 7751
8422 8532 8642 8752 8862 9533 9643 9753 9863 9973
共有20个解,将它们重排求差一次就可得到黑洞数,这里称它们为1步数。顺便指出,在类型1中逆推ABCD可有(10-m)(m-n)个解(最多可有25个解)。但这并不是说只有这20个数才是1步数。实际上,凡是与这20个数中任何一个数的构成数字相同的一般4位数,都是1步数。以6200为例,与之构成数字相同的6020、2060、2600、0262、0062等等也都是1步数,因为在重排求差时,它们的最大数都是6200。可见,每个最大数实际代表的都是一个等效数组。用排列组合法可以计算出这些等效数组一共包含了多少个一般的1步数。当构成数字均不相同时,4个数字可组成24个不同的4位数;当构成数字只有2个相同时,则可组成12个不同的4位数;如果构成数字两两相同,则可组成6个不同的4位数;如果构成数字有3个都相同,则可组成4个不同的4位数。据此计算, 1步数共有384个,显然,它们是各不相同的。
如果用其它差数逆推可以发现只有由6174逆推时才有与它构成数字相同的最大数7641,所以只有唯一的6174才是黑洞数,这就是证明黑洞数的第三种方法,显然此法比较麻烦。但逆推的最初用意并不在此。
2、类型2的逆推求解公式
当4位数mnpk满足条件m+k=9,m<9,n=p=9,时可用以下公式逆推求ABBD:
A= m+1+α (α = 0,1,2,……8-m)
B = β (β =α,α+1,α+2,……α+m+1)
D = α
α、β的取值法则与类型1相似,也是先使α从0开始一直取到8-m(A和D由此而定),在同一α条件下,β大多可取多个值,即从α一直取到α+m+1时为止。以mnpk=1998为例,此时m=1,写成式子和数表就是:
A= m+1+α = 2+α = 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 8 8 8 9 9 9
B = β = 0 1 2 1 2 3 2 3 4 3 4 5 4 5 6 5 6 7 6 7 8 7 8 9
D = α = 0 0 0 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7
将各数写成正规数的形式就是
2000 2110 2220 3111 3221 3331 4222 4332 4442 5333 5443 5553
6444 6554 6664 7555 7665 7775 8666 8776 8886 9997 9887 9997
共有24个解。一般地,此类型共有(9-m)(m+2)个解(最多可有30个解)。同样,这24个数都是最大数形式,它们中的每个数实际都代表了一个等效数组。
四、步数
从任意一个4位数开始反复作重排求差操作,最后可得黑洞数,其间操作的次数就是步数。这里将经过1次、2次、3次……操作可得黑洞数的数分别称为1步数、2步数、3步数等等。上面用黑洞数6174逆推得到的20个等效数组或384个一般4位数,只经过1次操作就得到黑洞数,故为1步数,它们距黑洞数最近,仅一步之遥。实践中已经发现,距黑洞数最远的是7步数(下面将给予证明),它们要经过7次操作才能到达黑洞数。黑洞数本身不经过操作就是黑洞数,操作任意次得到的仍然是黑洞数,故黑洞数本身可以是任意步数的数。
其它步数的数都可用逆推法求得。如果将1步数作为差数mnpk逆推,所得最大数就应该是2步数了。但是,并非所有1步数都能作为差数,它必须满足m+k=10、n+p=8、m>n或者m+k=9、m<9的条件,因而需要在1步数中去寻找。当然也不必将所有384个1步数都罗列出来,只需观察20个最大数,看看有哪些数直接满足条件,或者打散重排后能满足条件就行了。结果发现,8532、8352和4176能满足条件(黑洞数6174除外),分别用它们逆推,就可得2步数。用同样的方法,在2步数中找出能符合差数条件的数逆推,就可得3步数……如此逆推下去将可得所有步数的数,这就是提出逆推法的根本用意。最后发现,逆推了7次后,所有53个可能的差数(除黑洞数6174外)已被用尽,在最后所得的7步数中,已经没有符合差数条件的数了,这就证明不可能有8步数,最多7步。下面将各步数中合乎条件的mnpk列出来以供参考:
1步数中合乎逆推条件的数是:4176、8532、8352,用它们可逆推2步数。
2步数中合乎逆推条件的数是:2088、3087、4266、6264、7083、7353、7533、8082、9171、
9261、9621、9711,用它们可逆推3步数。
3步数中合乎逆推条件的数是:1089、1998、3996、4356、6354、6534、6993、8991、9081、
9801,用它们可逆推4步数。
4步数中合乎逆推条件的数是:0999、3177、5265、5355、5445、6444、7173、7443、8262、
8622,用它们可逆推5步数。
5步数中合乎逆推条件的数是:2178、2997、3267、4995、5994、7263、7623、7992、8172、
8712,用它们可逆推6步数。
6步数中合乎逆推条件的数是:4086、5085、5175、6084、8442、9351、9441、9531,
用它们可逆推7步数。
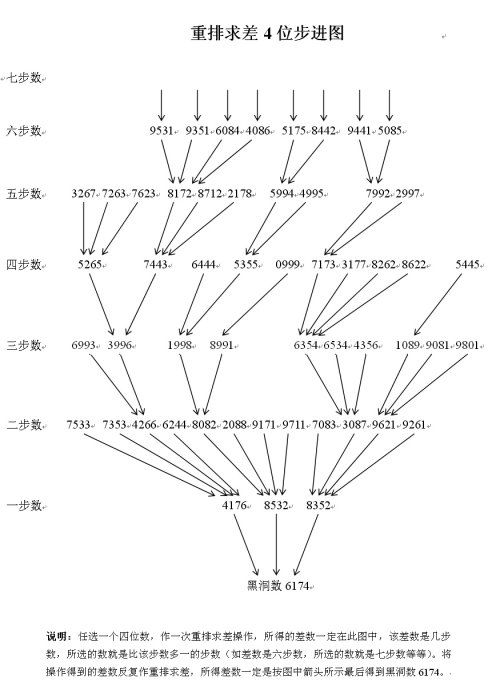
逆推过程不仅可得到所有步数的数,而且还将各步数间的步进关系也精确揭示了出来。任何一个4位数都是在重排求差过程中按部就班、有条不紊地步进到黑洞数的。本文后面附有所有步数的最大数表和差数步进图可以查阅,读者可在这些图表中找到另外一些有趣规律。
前已述及,任何一个最大数实际代表的都是一组数,并可通过它计算出它所代表的一般4位数的个数,而且,这样得到的4位数是互不相同的。下面就给出各步数的最大数和它们代表的一般4位数的个数:
1步数的最大数20个,一般数384个
2步数的最大数34个,一般数576个
3步数的最大数140个,一般数2382个
4步数的最大数129个,一般数1272个
5步数的最大数113个,一般数1530个
6步数的最大数153个,一般数1662个
7步数的最大数116个,一般数2184个
将1-7步数的一般数的个数加起来得9990,这正好是所有不同4位数的总个数(除4个数字相同者以外,共10个),就是说,所有4个数字不全相同的4位数,正好就构成了这1-7步数的所有4位数,或者反过来,1-7步数中所含4位数的总个数正好等于所有4个数字不全相同的4位数的总个数,它们都可通过1-7步重排求差得到黑洞数6174。这就证明了任何4位数均可重排求差得到黑洞数。
五、结论
通过最大数、最小数和它们的差数间的基本关系式可以证明,4位数在重排求差过程中,存在唯一一个黑洞数6174,从该黑洞数出发,可逐次逆推得到所有步数的数,这些数代表的一般4位数的总个数有、且只有9990个,它们正好是4个数字不全相同的4位数的总个数,就是说,4个数字不全相同的任何一个4位数总可通过重排求差操作按照严格的步进规律向着黑洞数收敛。
==================================================================================================
作者:nash_ 欢迎转载,与人分享是进步的源泉!
转载请保留原文地址:http://blog.csdn.net/nash_/article/details/8210686
===================================================================================================