POJ 3436 网络流 英文阅读题+技巧题
题目大意:
3 4 15 0 0 0 0 1 0 10 0 0 0 0 1 1 30 0 1 2 1 1 1 3 0 2 1 1 1 1组成acm电脑有3个零件,4种机器;
1号机器能产生15次,需要的3个零件:完全不需要(0:不需要,1:一定要,2:可要可不要);产出材料:产出一个单位的2号零件(1:生产该材料,0:不能生产该材料);
2号机器能生产10次,不需要零件,产出一个2,一个3号零件。
3号机器能生产30次,需要2号零件,3号零件可有可无,生产出1,2,3材料各一个。
4号机器.....
题目意思太晦涩了;或许是我英语不好的原因吧。
当某机器的产出与机器的需求能完全匹配上的话,则两台机器可以组成流水线。现在要求的就是:组成流水线产出的机器最大数。
so:
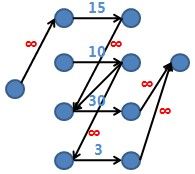
构图基本上就是这样:
直接求最大流,还是很简单的;
但是接下来的问题就是:
去找流边呢??
开始我的想法是:我做完了最大流之后,会有一些反边,也就是流过的边。这样做一次EK用bfs每次去找一条反向到汇点的路径,把这条路径存好就是了。
但是呢... 这样会存在问题:
因为我们一般写网络流已经不再把容量和流量概念放进代码里了,单单保存容量,每次对容量进行操作就可以了。但是这次单单进行简化的可不行了。
如果当前边有流量流过的话flow值一定是非零的。这就是一条可行路径。也就是流水线中间的一环。
所以,对网络流进行操作时,就必须还原到原始的状态,也就是要保存容量与流量。容量对流量进行限制,流量反应流的情况。
这样流完最大流之后,通过边的流量就可以获知机器的排布情况了。
当然可以通过cap与flow值进行bfs,但我们也可以简化思路,直接将有流量有容量的边输出即可。
另外提醒一点:2,也就是可要可不要零件,不能把它当成不要,看上去这种贪心思想是对的。实际上将2变成0,会引起机器之间的不匹配。导致原本可流的边不能流。
CODE:
#include<iostream>
#include<cstdio>
#include<string>
#define INF 0x00FFFFFF
#define MN 111
#define CC(what) memset( what,0,sizeof(what) )
template<class T> void inline checkmin( T &a,T b ){ if( a>b||a==-1 ) a=b; }
using namespace std;
int maze[MN][MN],flow[MN][MN],pre[MN],cur[MN],dis[MN],gap[MN];
int P,N,s,t,NE;
struct node{
int u,v,a;
}E[MN*MN];
void setG()
{
int rec[MN][MN];
CC(maze);CC(rec);CC(flow);
s=0;t=2*N+2;
int i,j,k;
for( i=1;i<=N;i++ )
{
scanf("%d",&maze[i<<1][i<<1|1]);
for( int j=1;j<=2*P;j++ )
scanf("%d",&rec[i][j]);
}
for( i=1;i<=N;i++ )
{
for( j=1;j<=N;j++ )
{
if( i==j ) continue;
bool can=true;
for( int k=1;k<=P;k++ )
if( rec[i][k+P]!=rec[j][k]&&rec[j][k]!=2 ){
can=false;break;
}
if(can)
maze[i<<1|1][j<<1]=INF;
}
int cnt=0;
for( k=1;k<=P;k++ )
cnt+=(rec[i][k]&1);
if(cnt==0) maze[s][i<<1]=INF;
cnt=0;
for( k=P+1;k<=2*P;k++ )
cnt+=rec[i][k];
if(cnt==P) maze[i<<1|1][t]=INF;
}
}
/*
int sap()
{
CC(pre),CC(cur),CC(gap),CC(dis);
int u=cur[s]=s,maxflow=0,aug=-1;
gap[0]=t+1;
while( dis[s]<=t ){
loop:
for( int v=cur[u];v<=t;v++ )
if( maze[u][v]-flow[u][v]&&dis[u]==dis[v]+1 )
{
cur[u]=v;
checkmin(aug,maze[u][v]-flow[u][v]);
pre[v]=u;
u=v;
if( v==t )
{
maxflow+=aug;
for( u=pre[u];v!=s;v=u,u=pre[u] )
flow[u][v]+=aug,flow[v][u]-=aug;
aug=-1;
}
goto loop;
}
int mind=t+1;
for( int v=0;v<=t;v++ )
if( maze[u][v]&&mind>dis[v] ){
cur[u]=v;mind=dis[v];
}
if( --gap[dis[u]]==0 ) break;
gap[dis[u]=mind+1]++;
u=pre[u];
}
return maxflow;
}
*/
int vis[MN],que[MN],a[MN];
bool bfs()
{
CC(vis);CC(que);
int head=0,foot=0;
que[foot++]=s;a[s]=INF;vis[s]=true;
while( head<foot )
{
int u=que[head++];
for( int i=s;i<=t;i++ )
if( !vis[i]&&maze[u][i]-flow[u][i] )
{
pre[i]=u;
vis[i]=true;
que[foot++]=i;
a[i]=min(a[u],maze[u][i]-flow[u][i]);
if( i==t ) return true;
}
}
return false;
}
int work()
{
int maxflow=0;
while( bfs() )
{
int m=t;
maxflow+=a[t];
while( m!=s )
{
flow[pre[m]][m]+=a[t];
flow[m][pre[m]]-=a[t];
m=pre[m];
}
}
return maxflow;
}
int main()
{
while( scanf("%d%d",&P,&N)!=EOF )
{
setG();
printf( "%d ",work() );
int ans[MN*MN][3];int pathnum=0;
for( int i=1;i<t;i++ )
for( int j=1;j<t;j++ )
{
if( maze[i][j]>0&&flow[i][j]>0&&i/2!=j/2 )
{
ans[pathnum][0]=i/2;
ans[pathnum][1]=j/2;
ans[pathnum++][2]=flow[i][j];
}
}
printf( "%d\n",pathnum );
for( int i=0;i<pathnum;i++ )
printf( "%d %d %d\n",ans[i][0],ans[i][1],ans[i][2] );
}
return 0;
}