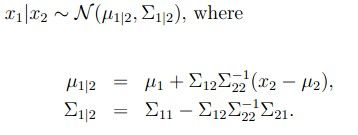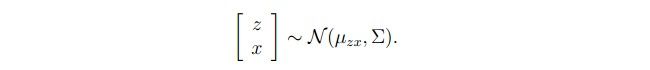机器学习 cs229学习笔记3 (EM alogrithm,Mixture of Gaussians revisited & Factor analysis )
(all is based on the stanford's open-course cs229 lecture 13)
接上次笔记 机器学习 cs229学习笔记2 (k-means,EM & Mixture of Gaussians)
如何确定EM算法converge呢?
当然是比较前后两次迭代的似然函数的大小,如果相差极小,则可以证明算法已经converge了
假设一次迭代开始时的参数是θ(t),迭代结束时的参数是θ(t+1)
因为我们之前对于Qi的选择保证了Jensen不等式的等号成立,所以对于θ(t)的似然函数就是
而θ(t+1)的似然函数则大于上式,原因很简单,因为θ(t+1)的取值是通过下图得到的
上面说明了EM算法是converge的
说实话:我感觉EM算法就是一种最大化似然函数的一个方法,因为原似然函数可能很难通过计算求出来
而EM取巧了,通过Jensen不等式,每次通过最大化一个下界,一次次逼近最大值。而这个下界往往很好求得。
也不知道对不对,还请知道的指教一下
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
Mixture Gaussians revisted:
这部分不想讲太多,其实就是反过去用EM算法的通式去推导出之前那个EM算法的特例
大家可以去看看note,需要的话就去看看note,讲得还是很详细的
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
这节课的视频其实很大一部分用来讲了EM算法的一些应用的推导,比如文本分类之类的
过程大体相似,下来之后我还是得自己思考着试图推一下,这里就不写太多了
然后讲到的就是Factor analysis,这是这节课的主要内容了
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
Factor analysis:
引入:
我们在执行EM formixture of gaussians的时候,绝大多数情况下样例数一定会比数据的维度大,即sample m >> dimension n
但是如果这个条件不满足的话(这是有可能的,比如文本分类的时候)
这时就会出现异常情况,如果n >> m,那么混合高斯函数的协方差矩阵∑就会变成奇异矩阵(singular),那么∑的逆矩阵就不存在
也就是说(1/|∑|^)(1/2)就会变成1/0,而这些都是计算时需要的
那么可以想到的方法之一就是对∑进行严格要求
1.严格要求∑为对角矩阵
这样multivariate gaussian的分布图像的等高线就会是一个圆形(二维中,如果是更高维则是高维中的sphere)
这样就会使算法失去一些有用的特性,同样也会出现一些参数上的方差为0而形成奇异矩阵
2.使∑为单位矩阵的倍数,倍数为所有样例的所有参数的方差之和
也就是在1的基础上进行更严格的要求,谨防一些参数上的方差为0而形成奇异矩阵
越严格要求∑,算法就会越死板,因而我们需要Factor analysis
在此之前先介绍一下多元高斯函数的边缘概率和条件概率
多元高斯函数的边缘概率和条件概率(待自证)
这里就直接给出一些公式了,因为我自己还没有推出来,andrew ng也是直接给的公式,等我看看再来补充这里吧(数学方面的确薄弱了些,准备加强)
其中,![]() ,x2类推
,x2类推
并且:
等我自己看懂再回来给出推导过程吧。。。。。。。。。。。。。(证明见此)
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
Factor analysis:
正文:factor analysis model 到底是啥呢
其实就是用更多的参数来捕获(capture)数据中间的关联关系,通过这些与普通混合高斯不同的参数来使协方差矩阵不至于奇异
那么首先给出下面推导需要的一些定义:
注意前两个式子 等价于 后面三个式子
其中z是隐含变量(latent variable)其实就是之前的y,也就是之前的Qi或者说w。
z是一个k维向量,k是混合高斯的个数(这里有问题,待修改),μ是一个n维向量,∧是一个n*k的矩阵,Ψ是一个n*n的对角矩阵
这个过程就是怎么弄的呢:1.想象x是由z生成的,将x映射到k维的仿射(affine)空间
2.加上ε的noise
也就是说将k维中z上的点映射到n维的空间中,而我们得到的数据x是n维的,所以如果得到了数据,则可以用这样一个model来fit数据
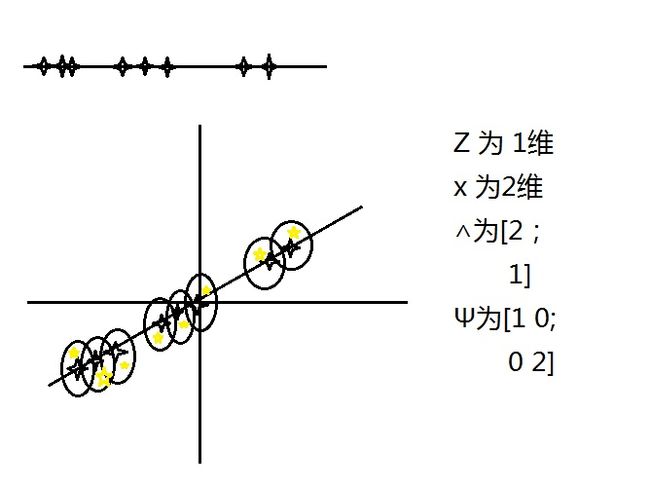
下面是一个实例:其中黄色的点就是我们得到的数据,而黑色的圆圈就是加上的noisy
factor analysis model就是给出黄色的点后我们试图去得到一个黑色的model,注意μ=0
给出这些定义之后,我们就可以得到:
通过上面多远高斯函数的式子,一层层计算就可以将上式演化成:(这部分推导很简单,就是将上面那个cov(x)的各项计算出来,因为其中的每个部分给的比较清楚,所以这部分略过了)
那么这样一个混合高斯的log似然函数就可以根据高斯函数的定义得到
显而易见,这货不好最大化,怎么最大化呢,当然是EM算法啦,这部分会在下节课中讲到。that's all
呼~~累死