排序算法整理(5)堆排序

程序参考了CLRS的《算法导论》，第六章 Heap Sort。

由于最大堆和最小堆是对称的，下文都说最大堆。

1 堆的定义

最大堆就是这样一种树，每个节点而言，如果它有儿子，那么此节点比它的儿子都大。

需要注意的有两点。

首先，堆几乎是一种完全二叉树，也可能是不完全的，下面第4部分中的图一。

其次，如果要用数组array来表示堆。那么必需两个元素，数组名和堆的大小heapsize。具体方式接下来解释。

第三，本文为了实现方便，忽略了array[0]。比如，如果要排序10个数，本文采取的方式是创建array[11]，用array[1], array[2], … ,array[10]来表示这10个数。

 2 堆排序的基本方法

堆排序的方法是

step 1把输入的数组改造成一个最大堆(使用max_heapify( )函数)

step 2 交换堆顶(最大元素)和堆底的最后一个元素

step 3 堆的大小heapsize减一

step 4 对剩下的元素重复step1 ~ step3的过程

3 创建堆的核心函数max_heapify

max_heapify是进行堆的创建和进行堆排序的核心函数。

可以递归和非递归两种方式来进行实现。

先说递归的方式，

max_heapify这个函数的输入是数组,array,下标index。

使用这个函数的前提条件是，由array[index]的左子树和右子树都已经是最大堆了。

但是array[index]可能并不比它的左儿子大，或者并不比它的右儿子大。此时需要调整array[index]和它的左儿子，右儿子的位置，使得array[index]和它的左儿子节点，右儿子节点，这3个节点重组为最大堆，也就说，array[index]比左儿子和右儿子中最大的那个儿子要大。

经过这次调整以后，array[index]和array[index]的左儿子，array[index]的右儿子构成了最大堆。但是，观察array[index]的左子树，左子树可能并不是一个最大堆了。于是，对左子树进行调整，递归地进行刚才的调整过程。或者，右子树可能不是一个最大堆了，同理应该对右子树进行调整。

再说非递归的方式。

如果非递归的进行，则从root到叶节点的方向，依次地进行每个节点和它的两个儿子的比较，不断地进行当前节点和左儿子(或者右儿子，取决于谁大)的比较，直到到了叶节点为止。

递归实现的代码如下

void max_heapify_recur(int * p_arr,int i,int heap_size) 
{
	int l = l_child(i);
	int r = r_child(i);
	int largest = 0;
	if ( (l<= heap_size) && (p_arr[l]>p_arr[i]) )
	    largest = l;
	else
		largest = i;
	if( (r<=heap_size) && (p_arr[r]>p_arr[largest]) )
		largest = r;
//	printf("i:%d,largest:%d,array[i]:%d,array[largest]:%d\n",i,largest,p_arr[i],p_arr[largest]);
	if (largest != i) {
		int temp = p_arr[i];
	    p_arr[i] = p_arr[largest];
		p_arr[largest] = temp;
		max_heapify_recur(p_arr, largest,heap_size);
	}
	return;
}

非递归实现的代码如下

void max_heapify_norecur(int * p_arr,int i,int heap_size) 
{
	while(i<=heap_size/2) {	
		int l = l_child(i);
		int r = r_child(i);
		int largest = 0;
		if ( (l<= heap_size) && (p_arr[l]>p_arr[i]) )
			largest = l;
		else
			largest = i;
		if( (r<=heap_size) && (p_arr[r]>p_arr[largest]) )
			largest = r;
//		printf("i:%d,largest:%d,array[i]:%d,array[largest]:%d\n",i,largest,p_arr[i],p_arr[largest]);
		if (largest != i) {
			int temp = p_arr[i];
			p_arr[i] = p_arr[largest];
			p_arr[largest] = temp;		
			i=largest;
		}
	}
	return;
}

4 创建堆的完整实现

首先应用一个小结论，如果一个堆有n个节点(用数组array[1] ,array[2]…,array[n]来表示)，那么这个堆的叶节点的下标是(int)n/2+1, (int)n/2+2…n 。（稍后另写一下对树相关的数量关系的总结）

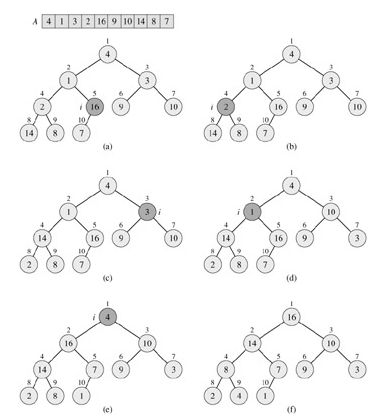
如果要构造一个最大堆，则从下标最大的非叶节点开始，到下标最小的非叶节点为止(到根节点为止)，逐步调用max_heapify即可。如下所示，偷来一张CLRS的配图。

即从index = (int) n/2开始，到index = 1为止，逐步调用max_heapify，

如下图，对10个元素进行排序，从index = 5开始，到index =1为止，逐步调用max_heapify。

                                                          图一

创建堆的代码如下

void build_heap(int * p_arr,int heapsize)
{
	int start=heapsize/2;
	for(int i = start;i>=1;i-- )
	{
		max_heapify_recur(p_arr,i,heapsize);
	}
	return;
}

5 堆排序的实现

假设待排序的有n个数，放在数组array[n+1]中，元素分别表示为array[1], array[2],…array[10]，为了方便，跳过了array[0]，从array[1]开始记录。

以n=10为例子来看。

对这array[1]这1个数，构造最大堆，显然根据定义和创建最大堆的过程，array[1]构成的最大堆也就是它自己了，最大节点在堆顶，为array[1]，交换array[1]和array[10]

发生交换后，对剩下9个数进行堆排序，此时的最大元素依然在堆顶，依然为array[1]，交换array[1]和array[9],

发生交换后，对剩下8个数进行堆排序，此时的最大元素依然在堆顶，依然为array[1]，交换array[1]和array[8],

..

发生交换后，对剩下2个数进行堆排序，此时的最大元素依然为array[1]，交换array[1]和array[2],

发生交换后，剩下1个数，没有排序的必要。

整理，输出数组。

代码如下

void heap_sort(int * p_arr, int length)
{
	int * adjusted_array =  new int[length+1];
	adjusted_array[0]=0;
	for(int i=0;i<length;i++) //构建下表从1开始的数组作为adjusted_array，方便进行堆排序
		adjusted_array[i+1]=p_arr[i];
	
	/*
	printf("测试1 排序前:\n");
	print_arr(adjusted_array,10);
	*/
	
	build_heap(adjusted_array,length);

	/*
	printf("测试2 创建heap后:\n");
	print_arr(adjusted_array,10);
	*/
	printf("\n\n");
	for(int heap_size=length;heap_size>=1;heap_size--) {		
		/*
		printf("heapsize is %d\n",heap_size);
		printf("测试3 交换前:\t");
		print_arr(adjusted_array,10);
		*/

		int temp = adjusted_array[1];
		adjusted_array[1] = adjusted_array[heap_size];
		adjusted_array[heap_size] = temp;	    
		max_heapify_recur(adjusted_array,1,heap_size-1);
		/*
		printf("测试4 交换后:\t");
		print_arr(adjusted_array,10);
		printf("\n");
		*/
	}

	for(int i=0;i<length;i++) //将adjusted_array还原为输入数组	
		p_arr[i]=adjusted_array[i+1];

	delete [] adjusted_array;
	return;
}

5 时间复杂度

max_heapify( )的时间复杂度为Olg(n) , 因为max_heapify( )的时间复杂度和堆的高度成线性关系，所以和lg(n)成线性关系。

创建堆的的时间负责度为O(n), CLRS《算法导论》第六章 上有证明，比较复杂，这里就不搬运了。

堆排序的的时间负责度为O(nlgn)，n个元素，每次挑出当前的最大的1个元素(时间复杂度为常数)，然后进行max_heapify( )操作(时间复杂度为lg(n))，所以时间复杂度为O(nlgn)。

6 堆数据结构的应用

下文, 排序算法整理(6)堆排序的应用，top K 问题 将讲讲堆这种数据结构的一个很奇妙的应用，top K问题，挑出一堆数中最大的K个数。