堆的节点总数n和叶结点数目的关系 (CLRS习题 6.1-7)

来自算法导论 CLRS的一个习题。Chapter 6 Heap Sort.  Exercise6.1-7

 

Show that, with the array representationfor storing an n-element heap, the leaves are the nodes indexed by ⌊n/2⌋ + 1, ⌊n/2⌋ + 2, . . . , n.

 

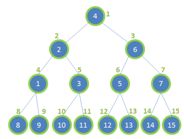
首先用一个例子来验证，如图1所示，

非叶节点有2⁰+2¹+2²=1+2+4=7个，叶节点有K+1 (2³=8)个。共有15个节点，叶结点开始于第8个，即第 [15/2]+1个，满足结论“叶结点开始于[n/2]+1”

然后开始证明，分为两种情况，完全二叉树和不完全二叉树。

证明之前先清楚高度的定义。一个节点的高度就是从这个节点到叶结点的路径包含的边的数目，树(包括二叉树，堆)的高度被定义为根节点的高度。

(1)如果是完全二叉树

如果是完全二叉树，假设非叶节点有K(2⁰+2¹+2²=1+2+4=7)个，叶节点有K+1 (2³=8)个。

假设完全二叉树的高度为h，则

非叶子节点的数目2⁰+2¹+2²+…+2^h-1=2^h-1

叶子节点的数目2^h

全部节点的数目2^h+1-1

如果用n表示全部节点的数目，则n = 2^h+1 –1 = 2^h – 1 + 2^h。显然叶子节点开始于[n/2]+1

 

(2)如果是不完全二叉树

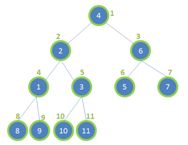
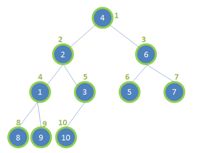
假设不完全二叉树的高度为h，不完全二叉树显然是通过完全二叉树转化而来的。如图2和图3把完全二叉树的叶结点摘掉几个，就成为了不完全二叉树。

              

                          图2                                                                          图3

(2.1)摘掉2k个叶结点

假设摘掉了2k个叶结点，如图2。那么原来的2k个叶结点就没有了，并且，这2k个叶结点的k个父节点也转化为了叶结点。这意味着，非叶节点减少了k了，叶结点减少了2k个，增加了k个，所以一共减少了k个。此时，

非叶子节点的数目2⁰+2¹+2²+…+2^h-1–k=2^h–1–k

叶子节点的数目2^h–k

全部节点的数目2^h+1–2k–1

如果用n表示全部节点的数目，则n = (2^h–1–k) + (2^h–k) = 2(2^h–1–k)+1，扣除前面的非叶子节点2^h–1–k个之后， 显然叶子节点开始于[n/2]+1

 

(2.2)摘掉2k+1个叶结点

假设摘掉了2k+1个叶结点，如图3，那么原来的2k+1个叶结点就没有了，并且，这2k+1个叶结点的k个父节点也转化为了叶结点。这意味着，非叶节点减少了k了，叶结点减少了2k+1个，增加了k个，所以一共减少了k+1个。此时，

非叶子节点的数目2⁰+2¹+2²+…+2^h-1–k=2^h–k–1

叶子节点的数目2^h–k–1

全部节点的数目2^h+1–2k–2

如果用n表示全部节点的数目，则n = (2^h–k–1) + (2^h–k–1) = 2(2^h–k–1)，则扣除前面的非叶子节点2^h–k–1个之后，不用取整刚好剩下n/2个节点，正是叶子节点。所以叶子节点开始于[n/2]+1