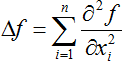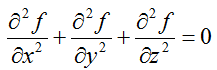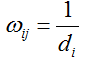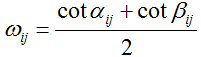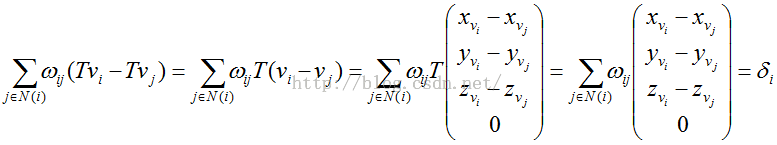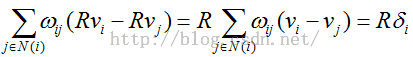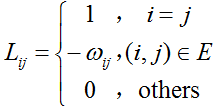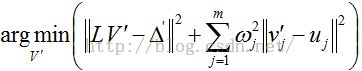图形处理(三)简单拉普拉斯网格变形-Siggraph 2004
简单拉普拉斯网格变形
原文地址:http://blog.csdn.net/hjimce/article/details/46415239
作者:hjimce
三角网格变形一直是CAGD相关领域的重点,刚上研究生的时候,感觉有点神奇。而且一上来导师就给我发了一篇基于格林坐标的自由变形的相关paper,让我看,外文文献,看了n多天,第一次看外文文献,啥也没看懂,好像也没什么收获。因为当时根本连文献要怎么看都不懂,如何把一篇文献转换成代码,更别谈直接看外文文献了,一篇文章下来,根本不知道哪里是重点……之所以把这篇博文标题为:简单拉普拉斯网格变形,是因为我只用了求解一个稀疏的线性方程组,就进行变形。
本篇博文主要是参考阅读2004年Siggraph上面的几篇微分网格变形的相关文献:《Laplacian Surface Editing》、《Differential Coordinates for Interactive Mesh Editing》……因为2004年,各路大神刚研究出了微分变形的算法,所以有很多篇Siggraph的paper都很牛逼……
一、 拉普拉斯坐标相关理论
拉普拉斯网格变形的本质是网格模型局部细节特征的编码和解码的过程。编码过程是指网格顶点的欧氏空间坐标到Laplacian坐标的转换。Laplacian坐标包含了网格的局部细节特征,因此Laplacian网格变形算法能够较好地保持网格模型的局部细节。解码过程是指通过微分坐标反求欧氏空间坐标,实质上是一个求解线性系统的过程。因此Laplacian网格变形算法高效、鲁棒。
1、曲面拉普拉斯算子(参考文献基于微分坐标的网格morphing)
拉普拉斯算子是n维欧几里德空间中的一个二阶微分算子,被定义为梯度(![]() )的散度(
)的散度(![]() ),因此如果是二阶可微的实函数,则的拉普拉斯算子定义为:
),因此如果是二阶可微的实函数,则的拉普拉斯算子定义为:
的拉普拉斯算子也是笛卡尔坐标系xi中的所有非混合二阶偏导数:
对于三维欧式空间中的拉普拉斯方程为:
其中,为三维空间中二阶可微的实函数。
上次常简写为:
![]()
2、 离散拉普拉斯坐标
拉普拉斯坐标蕴含着曲面的局部特征信息,网格曲面的拉普拉斯坐标其在网格变形、网格平滑、网格去噪等方面都用着重要的应用。
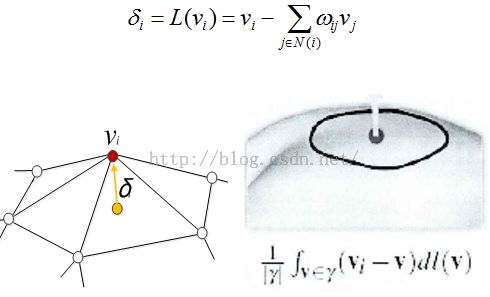
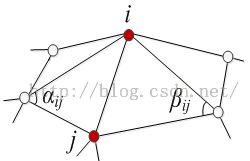
给定具有n个顶点的三角网格模型M=(V,E,F),V为顶点集,E为边集,F为三角面片集合。设v1,…vn为点集V中的点,对于每个顶点vi,用传统的笛卡尔坐标表示,记vi=(xi,yi,zi);用N(i)={j|(i,j)∈E},表示第点的1-ring邻域顶点构成的集合,如图1,定义vi处的拉普拉斯坐标为:
其中,δi为顶点vi的拉普拉斯坐标,L(·)为网格的拉普拉斯算子,ωij为vj点相对于vi点的权值,且∑ωij=1。目前常用的权值包括均匀权值、余切权值、正切权值、弹簧权值等。
(1)均匀权值计算公式:
其中,di为顶点vi的度(邻接顶点的个数),由于这种权值只是简单的平均,故又称为均匀权值,采用该权值进行网格变形时,所获得的精度较低。
(2)余切权值计算公式:
其中,αij、βij是边vivj的两个邻接三角面片的对角,如图所示。
本文采用余切权值进行相关计算,可获得较好的网格变形结果。
3、 拉普拉斯坐标的性质
(1)线性变换(参考自拉普拉斯坐标在网格变形中的应用)
若T是点集V的线性变化,则
![]()
(2)平移不变性
若T是平移变换,则
(3)对旋转变换敏感
若R是旋转变换,则
二、 拉普拉斯网格变形框架
对于有n个顶点的网格模型M,由公式(1)式简写成矩阵形式为:
![]()
其中,
L为n×n的拉普拉斯矩阵,其秩为n-k,其中k是M连通子集的个数,且
拉普拉斯网格变形的本质是通过求解线性方程组公式1,获得变形后网格模型的顶点坐标V'。然而由于公式1的拉普拉斯矩阵是不可逆矩阵,其秩为n-k,因此需要至少增加k个顶点的坐标作为约束条件,方程组1才有解,这些约束顶点我们称之为约束点(“锚点”)。
在交互式网格变形编辑中,一般是由用户鼠标点选约束点。如图1,我用户交互输入v1,v2作为约束顶点,然后鼠标拖动v2点,可实现球体模型的实时变形。
设M中的部分顶点vj作为约束条件,其变形后的绝对坐标v'j已知,v'j = uj,j=1, 2, …, m,m为约束顶点的个数(m≧k)。基于拉普拉斯坐标的网格变形方法获得变形后的顶点V',可归结求解一个带位置约束的优化问题:
式中 wj ——约束点权值
解(3)中的最小值问题,就相当于求解下面的超静定线性系统
其中,
Δ'的每一列表示每个顶点对应的拉普拉斯坐标。H是m×n阶矩阵,H的每一行只有一个非零元素,其值为对应的约束权值。h为m×3阶矩阵,即![]() ,每列代表一个坐标分量。未知数V'是的矩阵
,每列代表一个坐标分量。未知数V'是的矩阵![]() ,其第i行表示变形后的网格顶点的三维坐标
,其第i行表示变形后的网格顶点的三维坐标![]() ,这样求解该线性系统,可获得变形后各顶点的坐标。
,这样求解该线性系统,可获得变形后各顶点的坐标。
公式(1)是一个超静定方程组,根据超静定方程组的求解方法,其等价于求解下式:
可得:
通过上式可求得各个网格顶点的三维坐标。
根据拉普拉斯坐标的性质,由于拉普拉斯坐标对旋转敏感,使得网格的局部信息会发生旋转扭曲,特别是对于大尺度变形时,其扭曲尤为严重。如图3所示,原网格模型本来为圆形的特征,经过变形后圆形特征发生严重扭曲。也就是说要实现网格模型的保特征变形,不能直接使用原网格的拉普拉斯坐标来重建变形后的网格模型,而应该重新设置微分坐标的方向再重建模型,下一节将具体介绍如何求取未知的拉普拉斯坐标。由于拉普拉斯坐标不具有旋转不变性,简单地用原始的拉普拉斯坐标Δ近似未知变换网格的拉普拉斯坐标Δ',很容易产生扭曲变形,如图3 所示(Differential Coordinates for Interactive Mesh Editing):
总结:三角网格曲面的变形算法中,现在效果最好的是微分变形,当然现在的很多商业软件,三维的建模软件的变形算法并不是用了微分变形算法,而是使用自有变形,这个在proe软件中就有类似的功能,自由变形的优点是它的速度快。不过对于微分变形,虽然需要求解一个大型的稀疏矩阵,但是这个矩阵现在有一些快速的解法,就像二维图像泊松融合一样,有快速求解泊松方程的算法,所以总的来说,现在微分域的变形算法,是最有前途的。本篇博文中,我只讲解了简单的拉普拉斯微分变形算法,没有对拉普拉斯坐标的方向问题进一步的讲解,因为现在研究比较多的就是如何求解拉普拉斯坐标的新方向,这个可以用旋转不变量、调和场等方法,具体后续再进行详解。
参考文献:
1、《Differential Coordinates for Interactive Mesh Editing》
2、《基于微分坐标的网格morphing》
3、《 Dual Laplacian editing for meshes》
4、《Linear rotation-invariant coordinates for meshes》
5、《 Differential coordinates for interactive mesh editing》
6、《拉普拉斯坐标在网格变形中的应用》
**********************作者:hjimce 时间:2015.7.15 联系QQ:1393852684 地址:http://blog.csdn.net/hjimce 原创文章,版权所有,转载请保留本行信息********************