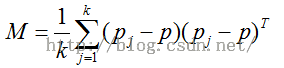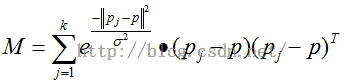图形处理(九)点云重建(下)法矢求取、有向距离场等值面提取
一、相关理论
在点云重建算法中,点云法矢的求取是非常重要的一步。之前导师让我做点云尖锐特征边重建时,发了一堆异向法矢求取的英文paper,当时我很迷糊,就问了老师,让我做点云重建,为什么发的文献资料都是关于法矢求取的。原来法矢求取,直接关系着重建效果,废话不多说。
点云重建的一般步骤是:
1、点云预处理 。这一步主要是点云滤波、采样、移除离群点等操作,涉及到的经典算法有MLS、双边滤波、WLOP等,这些在我的另外一篇博文中,有比较详细的介绍。
2、重建网格曲面。这一步主要涉及相关经典算法是点云法矢求取PCA、有向距离场、隐函数、MC算法等相关概念。这篇博文将详解这些算法的实习过程。
二、重建算法流程
重建网格曲面算法流程:
1、通过KD树,求取点云的每个点Pi的k近邻点,对于k值得选取,需要根据点云的密度进行自适应效果会比较好。我比较常用的值是8、16……
这一步可以从网上下载flann库,进行调用,当然如果你熟悉PCL点云开源处理库,那后续的步骤都只是调用一个函数的事了。这一步的代码就不贴了,就是把点云的每个点的k近邻求取出来就完事了。
2、根据k近邻进行计算点云法矢。法矢的初步估算这一步经典的算法是PCA算法,PCA算法是点云法矢计算的常用算法。
a.均匀权的pi点法矢计算公式为:
其中pj为p点的k近邻。然后通过求解协方差矩阵M的最小特征值的特征向量,作为p点的法向量,这就是所谓的主元分析方法PCA。
b.基于高斯权重的主元分析方法:
原来的方法,采用的是均匀权重的方法(1/k),把均匀权改为高斯权:
通过求解M的最小特征值的特征向量,获得p点的法向量,其中参数σ可以选择跟点云密度相关的参数。
具体σ的计算方法,我是用了paper:Efficient Simplification of Point-Sampled Surfaces,的相关方法进行计算的,代码如下:
int vn=m_Tmesh->vertices.size();
if(vn==m_Radius.size())return;
m_Radius.resize(vn);
for (int i=0;i<vn;i++)
{
float max_dist=0;
for (int j=0;j<m_Tmesh->neighbors[i].size();j++)
{
float nei_dist=len2(m_Tmesh->vertices[m_Tmesh->neighbors[i][j]]-m_Tmesh->vertices[i]);
if (nei_dist>max_dist)
{
max_dist=nei_dist;
}
}
m_Radius[i]=sqrt(max_dist)/3;//估计方法见Efficient Simplification of Point-Sampled Surfaces
}
上面的m_Radius代表的就是σ了。于是根据上面点云每个顶点法矢的求解公式,可以写出代码如下:
for (long i = 0; i < nv; i++)
{
//计算C矩阵,也就是协方差矩阵
double C[3][3] = { {0,0,0}, {0,0,0}, {0,0,0} };
for (int ni=0; ni<m_Tmesh->neighbors[i].size();ni++) //遍历点云的k近邻顶点
{
int ind =m_Tmesh->neighbors[i][ni];
vec d = vertices[ind]-vertices[i];
float weight_distance=exp(-len2(d)/(m_Radius[i]*m_Radius[i]));//m_Radius[i]是点云当前点i的密度
for (int l = 0; l < 3; l++)
for (int m = 0; m < 3; m++)
{
C[l][m] +=weight_distance*d[l] * d[m];//高斯权重
}
}
//对协方差矩阵C进行特征值分解
Array2D<double> jz(3,3);
for (int l=0; l<3; l++)
{
for(int j=0;j<3;j++)
{
jz[l][j]=C[l][j];
}
}
Eigenvalue<double> aa(jz);//特征值分解可以调用Eigen库比较方便
Array2D<double> CC(3,3);
//获取分解结果,协方差矩阵的三个特征向量
aa.getV(CC);
m_Tmesh->normals[i]=vec(CC[0][0],CC[1][0],CC[2][0]);//第一列向量就是最小特征值对应的特征向量
if(len2(m_Tmesh->normals[i])>1e-10)normalize(m_Tmesh->normals[i]);//法矢归一化
}
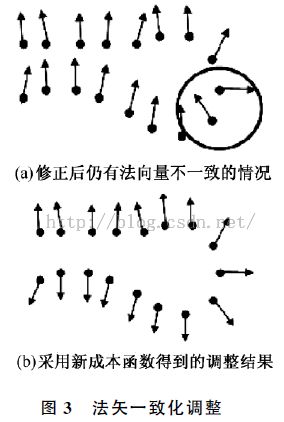
C、法矢方向一致化
定义成本函数:
通过上面的特征向量的方法,求解出来的法矢,其实是不具有方向统一性的。假设每个点的最小特征值对应的特征向量,然后归一化后,法矢为V,然而其实:-V也是法矢。因此我们需要对所以得顶点,规定一个统一的方向,比如让所有的法矢朝向曲面的外部。因此需要做统一的法矢方向归一化处理,这一步也叫法矢方向一致化,主要用MST算法。
算法首先为点云所以顶点,定义一个成本函数:
d为从点p指向点q的单位向量,np、nq分别为点p、q的法矢,p、q是邻接顶点,这一步的代码如下:
// 3a. Compute a cost between every pair of neighbors for the MST
// cost = 1 - |normal1.normal2|
//
vector< vector<float>>costs(nv);
for (int i=0;i<nv;i++)
{
costs[i].resize(m_Tmesh->neighbors[i].size());
}
bool cost_method=true;
#pragma omp parallel for
for(int i=0;i<nv;i++)
{
int m=m_Tmesh->neighbors[i].size();
for(int j=0;j<m; j++)
{
//文献Consolidation of Unorganized Point Clouds for Surface Reconstruction 4.1的公式
float ndot=m_Tmesh->normals[i] DOT m_Tmesh->normals[m_Tmesh->neighbors[i][j]];
float f;
if (cost_method==false)
{
vec vpq1=vertices[m_Tmesh->neighbors[i][j]] - vertices[i];
normalize(vpq1);
f=fabs(vpq1 DOT m_Tmesh->normals[i])+fabs(vpq1 DOT m_Tmesh->normals[m_Tmesh->neighbors[i][j]]);
}
else
f= 1.0- fabs(m_Tmesh->normals[i] DOT m_Tmesh->normals[m_Tmesh->neighbors[i][j]]) ;
costs[i][j]=f;
}
}
成本函数有的时候,在有的其他paper中也可以定义为:cost = 1 -|np.nq|
有了成本函数以后,接着就要以这个为法矢方向调整的依据了,进行广度优先遍历。
MST算法实现:
首先从点云模型中,选择z值最大的点,作为广度优先遍历的种子点,调整种子点的法矢方向,使得其与向量(0,0,1)的夹角小于0,这样可以保证最后所有的点云的法矢指向曲面的外侧。
接着以成本函数为权值,遍历点云广度优先遍历点云,由i点遍历到其邻接顶点j时,如果:
ni*nj<0
那么将j点的法矢调整方向,否则nj方向不需要调整。代码实现如下:
// 3b. 法矢方向一致化
int orientationPropagation=1;
if(orientationPropagation)
{
vector<int> nearby ; //未被访问的邻接顶点
int first=0; //选择索引为0的点,作为遍历的种子点
isVisited.resize(nv);
isVisited[first] = 1;
nearby.reserve(m_Tmesh->neighbors[first].size());
for(int j=0;j<m_Tmesh->neighbors[first].size();j++)
{
int nid=m_Tmesh->neighbors[first][j];
nearby.push_back(nid);
}
double cost,lowestCost;
int cheapestNearby = 0, connectedVisited = 0;
// 直到所有的点全部被遍历完毕
while(nearby.size()>0)
{
// 对于每个邻接顶点而言:
int iNearby,iNeighbor;
lowestCost = 1.0e+100;
for(int i=0; i<nearby.size(); i++)
{
iNearby = nearby[i];
for(int j=0;j<m_Tmesh->neighbors[iNearby].size();j++)
{
iNeighbor = m_Tmesh->neighbors[iNearby][j];
if(isVisited[iNeighbor])
{
cost = costs[iNearby][j];
if(cost<lowestCost)
{
lowestCost = cost;
cheapestNearby = iNearby;
connectedVisited = iNeighbor;
if(lowestCost<0.05)
{
i = nearby.size();
break;
}
}
}
}
}
//法矢点乘小于零 那么需要方向调整
if((m_Tmesh->normals[cheapestNearby] DOT m_Tmesh->normals[connectedVisited])<-1e-10)
{
m_Tmesh->normals[cheapestNearby]=(-1.0f)*m_Tmesh->normals[cheapestNearby];
}
isVisited[cheapestNearby]= 1;
//移除已然被访问的点
vector<int>::iterator iter;
iter=find(nearby.begin(),nearby.end(),cheapestNearby);
nearby.erase(iter);
// 加入未被访问的顶点
for(int j=0;j<m_Tmesh->neighbors[cheapestNearby].size();j++)
{
iNeighbor = m_Tmesh->neighbors[cheapestNearby][j];
if(isVisited[iNeighbor] == 0)
{
vector<int>::iterator iter1;
iter1=find(nearby.begin(),nearby.end(),iNeighbor);
if (iter1==nearby.end())
{
nearby.push_back(iNeighbor);
}
}
}
}
nearby.clear();
}
当然求得点云法矢后,建议进行法矢平滑处理,这样最后重建的效果会好一些,具体可以参考我的另外一篇博文。
3、对点云的最小包围盒(bbox)进行体素网格划分。
这一步不解释,知道三维体素的人都懂,基础知识,具体体素要划分的多细得看你的需求,可以用点云模型的bbox,进行x,y,z轴三个方向的划分,比如可以各个方向划分1000个刻度,当然刻度多大,还是得看点云模型的尺度大小的,或者你可以先求出点云的密度的统计,在根据密度的大小进行划分。
4、求取体素的八个顶点的有向距离场。
将切平面作为待重建曲面M,可以构造体素点到M的有向距离函数为:
![]()
xi为点云模型顶点,与p的最近点,ni为i点对应的法矢。这样就相当于求取p点到曲面的近似最短距离了,当然这个距离是有向的,如果点p位于M的外面,那么它的有向距离应该是正的,否则为负值。
也就是说这一步我们需要计算每个体素顶点p到曲面的最短距离,而最短的距离的计算,就是通过计算p的最近点xi,xi为点云顶点,p到xi的最短距离,就相当于其到xi切平面的距离。
//计算有符号距离
void DataSets::signed_distance()
{
vector<vec>& vertices=m_Tmesh->vertices;
int vn= vertices.size();
if(!vn) return;
for(long i=0;i<3;i++)
{
bounds[i*2]-=this->SampleSpacing*1.5;
bounds[i*2+1]+=this->SampleSpacing*1.5;
}
topleft[0] = bounds[0];
topleft[1] = bounds[2];
topleft[2] = bounds[4];
bottomright[0] = bounds[1];
bottomright[1] = bounds[3];
bottomright[2] = bounds[5];
for(int i=0;i<3;i++)
{
dim[i] = int((bottomright[i]-topleft[i])/this->SampleSpacing+1);
}
float *v0 = &vertices[0][0];
KDtree *kd = new KDtree(v0, vn);
sd=new float[dim[0]*dim[1]*dim[2]]; //存储各点的有符号距离
m_direction_field.clear();
m_direction_field.resize(dim[0]*dim[1]*dim[2]);
float radius=16.0*SampleSpacing;
float radius1=3.0*rou;
int count_cute=0;
for(int z=0;z<dim[2];z++)
{
for(int y=0;y<dim[1];y++)
{
for(int x=0;x<dim[0];x++)
{
float xx = topleft[0] + x*this->SampleSpacing;
float yy=topleft[1] + y*this->SampleSpacing;
float zz = topleft[2] + z*this->SampleSpacing;;
long iClosestPoint;
vec pointp(xx,yy,zz);
const float *match = kd->closest_to_pt(pointp, radius);
if(match) iClosestPoint = (match - v0) / 3;
else
{
sd[count_cute]=UNDEF;
m_direction_field[count_cute]=vec(UNDEF,UNDEF,UNDEF);
count_cute++;
continue;
}
vec vectorp=pointp-vertices[iClosestPoint];
vec plane_normal(m_Tmesh->normals[iClosestPoint][0],m_Tmesh->normals[iClosestPoint][1],m_Tmesh->normals[iClosestPoint][2]);
float dist_plane=vectorp DOT plane_normal;
sd[count_cute]=dist_plane;
m_direction_field[count_cute]=dist_plane*plane_normal;
count_cute++;
}
}
}
delete kd;
}
5、根据体素的八个顶点的符号,结合MC算法,确定求交关系。
因为我们上面求解的是有向距离场,也就是说每个体素有八个顶点,其八个顶点通过上一步我们可以求得有向距离场。那么MC算法的等值面的提取原理是什么呢?
其实如果一个体素,与待重建的曲面相交,那么该体素的8个顶点的有向距离,肯定会有正有负。因此我们只需要处理那种8个顶点中有正有负的体素就可以了。而MC算法就是根据相交情况,进行查表,得到相交的三角网格模型的。
首先对体素的8个顶点进行分类,以判断其顶点是位于等值面之外,还是位于等值面之内。再根据8个顶点的状态,确定等值面的剖分模式。顶点分类规则为:
1)如体素顶点的数据值大于或等于等值面的值,则定义该顶点位于等值面之外, 记为正点,即“1“
2)如体素顶点的数据值小于等值面的值,则定义该顶点位于等值面之内,记为负点, 即“0"
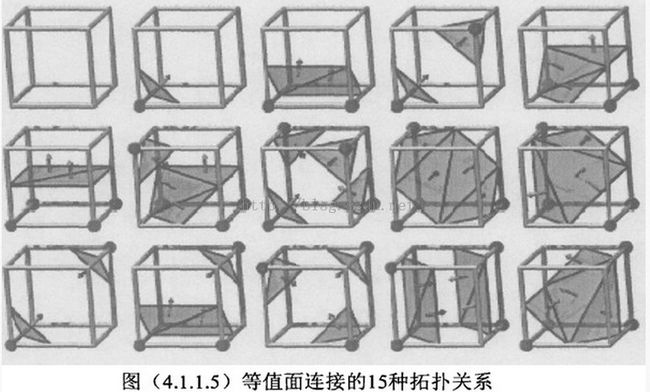
由于每个体素共有8个顶点,且每个顶点有正负两种状态,所以等值面可能以 =256种方式与一个体素相交。通过列举出这256种情况,就能创建一张表格,利用它可以查出任意体素中的等值面的三角面片表示。如果考虑互补对称性,将等值面的值和8个角点的函数值的大小关系颠倒过来,即将体素的顶点标记置反(0变为1, 1变为0),这样做不会影响该体素的8个角点和等值面之间的拓扑结构,可将256种方式简化成128种。其次,再利用旋转对称性,可将这128种构型进一步简化成15种。图3.2给出了这15种基本构型[131其中黑点标记为“1”的角点。
根据8个顶点有向距离场,的正负情况进行查表,可以得到三角面片。然后三角面片的顶点的坐标,也就是体素点边与待重建曲面的相交点,这个可以用体素点边的两个顶点进行线性插值得到,网格曲面每个顶点的坐标。
于是有了网格曲面的每个顶点,也有了三角面片,这样网格曲面也就重建完毕了。OK算法至此结束。
参考文献:
1、《基于点云的鞋楦三角网格曲面重构》
2、《点云模型法矢优化调整》
本文地址:http://blog.csdn.net/hjimce/article/details/46419179 作者:hjimce qq:1393852684 更多资源请关注我的博客:http://blog.csdn.net/hjimce 原创文章,版权所有,转载请保留本行信息