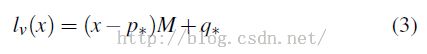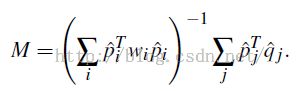图像处理（十九）基于移动最小二乘的图像变形-Siggraph 2006

基于移动最小二乘的图像变形

原文地址：http://blog.csdn.net/hjimce/article/details/46550001

作者：hjimce

一、背景意义

写这篇博文是应为目前为止我看到了好多领域里的经典paper算法都有涉及到移动最小二乘（MLS）。可见这个算法非常重要，先来看一下它的相关经典应用：

1、图像变形。在图像处理领域paper：《Image Deformation Using Moving Least Squares》利用移动最小二乘的原理实现了图像的相关变形，而且这篇paper的引用率非常高，可以说是图像变形算法的经典算法，Siggraph上面的paper。

利用移动最小二乘实现图像变形

2、点云滤波。利用MLS实现点云滤波，是三维图像学点云处理领域的一大应用，我所知道点云滤波经典算法包括：双边滤波、MLS、WLOP。

3、Mesh Deformation。用这个算法实现三角网格模型的变形应用也是非常不错的，相关的paper《3D Deformation Using Moving Least Squares》

OK，接着我就以《Image Deformation Using Moving Least Squares》算法为例，进行讲解基于移动最小二乘的图像变形算法实现。

二、算法实现

在这里我没有打算将算法原理的推导过程，直接讲算法的实现步骤公式。

这篇paper根据变换矩阵的不同，可以分为三种变形方法，分别是仿射变换、相似变换、刚性变换。其中刚性变换的效果是最好的，我这边从简单的讲，只讲仿射变换的变形算法实现：

问题：原图像的各个控制顶点坐标p，原图像上的像素点v的坐标。变形后图像的控制顶点位置q，求v在变形后图像中对应位置f(v)。

总计算公式为：

上面中lv(x)和f(v)是同一个函数。因为x就是我们输入的原图像的像素点坐标v。

因此我们的目标就是要知道p*，q*，变换矩阵M。这样输入一个参数x，我们就可以计算出它在变换后图像中的位置了。

OK，只要我们知道上面公式中，各个参数的计算方法，我们就可以计算出变形后图像对应的坐标点f(v)了。

1、权重w的计算方法为：

也就是计算v到控制顶点pi的距离倒数作为权重，参数a一般取值为1。

这一步实现代码如下：

	//计算各个控制顶点的权重，也就是计算点t到各个顶点的距离1/sqr(d)
	while(iter!=p.end())
	{
		double temp;
		if(iter->x!=t.x || iter->y!=t.y)
		    temp=1/((iter->x-t.x)*(iter->x-t.x)+(iter->y-t.y)*(iter->y-t.y));
		else//如果t为控制顶点，那么需要把该控制顶点的权重设置为无穷大
			temp=MAXNUM;
		w.push_back(temp);
		iter++;
	}

2、q*，p*的计算公式如下：

也就是计算控制顶点pi和qi的加权求和重心位置。

	double px=0,py=0,qx=0,qy=0,tw=0;
	while(iterw!=w.end())
	{
	px+=(*iterw)*(iter->x);//所有控制顶点p的加权位置
	py+=(*iterw)*(iter->y);
	qx+=(*iterw)*(iterq->x);//所有控制顶点q的加权位置
	qy+=(*iterw)*(iterq->y);
	tw+=*iterw;//总权重
	iter++;
    iterw++;
	iterq++;
	}
	pc.x=px/tw;
	pc.y=py/tw;
	qc.x=qx/tw;
	qc.y=qy/tw;

3、仿射变换矩阵M的计算公式如下:

只要把相关的参数都带进去就可以计算了。

最后贴一些完整的MLS源代码：

//输入原图像的t点，输出变形后图像的映射点f(v)
MyPoint CMLSDlg::MLS(const MyPoint& t)
{
	if(p.empty())//原图像的控制顶点p，与输入点t为同一副图像坐标系下
		return t;
	MyPoint fv;
	double A[2][2],B[2][2],M[2][2];
	iter=p.begin();
	w.erase(w.begin(),w.end());
	//计算各个控制顶点的权重，也就是计算点t到各个顶点的距离1/sqr(d)
	while(iter!=p.end())
	{
		double temp;
		if(iter->x!=t.x || iter->y!=t.y)
		    temp=1/((iter->x-t.x)*(iter->x-t.x)+(iter->y-t.y)*(iter->y-t.y));
		else//如果t为控制顶点，那么需要把该控制顶点的权重设置为无穷大
			temp=MAXNUM;
		w.push_back(temp);
		iter++;
	}
	vector<double>::iterator iterw=w.begin();
	vector<MyPoint>::iterator iterq=q.begin();//q为目标图像的控制点的位置，我们的目标是找到t在q中的对应位置
	iter=p.begin();
	MyPoint pc,qc;
	double px=0,py=0,qx=0,qy=0,tw=0;
	while(iterw!=w.end())
	{
	px+=(*iterw)*(iter->x);//所有控制顶点p的加权位置
	py+=(*iterw)*(iter->y);
	qx+=(*iterw)*(iterq->x);//所有控制顶点q的加权位置
	qy+=(*iterw)*(iterq->y);
	tw+=*iterw;//总权重
	iter++;
    iterw++;
	iterq++;
	}
	pc.x=px/tw;
	pc.y=py/tw;
	qc.x=qx/tw;
	qc.y=qy/tw;
	iter=p.begin();
	iterw=w.begin();
	iterq=q.begin();
	for(int i=0;i<2;i++)
    for(int j=0;j<2;j++)
	{
	A[i][j]=0;
	B[i][j]=0;
	M[i][j]=0;
	}
	while(iter!=p.end())
	{

	double P[2]={iter->x-pc.x,iter->y-pc.y};
	double PT[2][1];
	PT[0][0]=iter->x-pc.x;
	PT[1][0]=iter->y-pc.y;
	double Q[2]={iterq->x-qc.x,iterq->y-qc.y};
	double T[2][2];
   
    T[0][0]=PT[0][0]*P[0];
    T[0][1]=PT[0][0]*P[1];
	T[1][0]=PT[1][0]*P[0];
    T[1][1]=PT[1][0]*P[1];

	for(int i=0;i<2;i++)
    for(int j=0;j<2;j++)
	{
	A[i][j]+=(*iterw)*T[i][j];
	}
	T[0][0]=PT[0][0]*Q[0];
    T[0][1]=PT[0][0]*Q[1];
	T[1][0]=PT[1][0]*Q[0];
    T[1][1]=PT[1][0]*Q[1];
    
	for(int i=0;i<2;i++)
    for(int j=0;j<2;j++)
	{
	B[i][j]+=(*iterw)*T[i][j];
	}

	iter++;
    iterw++;
	iterq++;
	}
	//cvInvert(A,M);
    double det=A[0][0]*A[1][1]-A[0][1]*A[1][0];
	if(det<0.0000001)
	{
		fv.x=t.x+qc.x-pc.x;
		fv.y=t.y+qc.y-pc.y;
		return fv;
	}
    double temp1,temp2,temp3,temp4;
	temp1=A[1][1]/det;
	temp2=-A[0][1]/det;
	temp3=-A[1][0]/det;
	temp4=A[0][0]/det;
	A[0][0]=temp1;
    A[0][1]=temp2;
	A[1][0]=temp3;
	A[1][1]=temp4;


	M[0][0]=A[0][0]*B[0][0]+A[0][1]*B[1][0];
	M[0][1]=A[0][0]*B[0][1]+A[0][1]*B[1][1];
	M[1][0]=A[1][0]*B[0][0]+A[1][1]*B[1][0];
	M[1][1]=A[1][0]*B[0][1]+A[1][1]*B[1][1];

	double V[2]={t.x-pc.x,t.y-pc.y};
	double R[2][1];
  
	R[0][0]=V[0]*M[0][0]+V[1]*M[1][0];//lv（x）总计算公式
	R[1][0]=V[0]*M[0][1]+V[1]*M[1][1];
	fv.x=R[0][0]+qc.x;
	fv.y=R[1][0]+qc.y;

	return fv;
}

调用方法示例：

    int i=0,j=0;
	dImage=cvCreateImage(cvSize(2*pImage->width,2*pImage->height),pImage->depth,pImage->nChannels);//创建新的变形图像
	cvSet(dImage,cvScalar(0));
	MyPoint Orig=MLS(MyPoint(IR_X,IR_Y));
	int Orig_x=(int)(Orig.x)-(int)(pImage->width/2);
	int Orig_y=(int)(Orig.y)-(int)(pImage->height/2);

	for(i=0;i<pImage->height;i++)//遍历原图像的每个像素
	{
		for(j=0;j<pImage->width;j++)
		{
			CvScalar color;
			double x=j+IR_X;
			double y=i+IR_Y;
			MyPoint t=MLS(MyPoint(x,y));//MLS计算原图像(x,y)在目标图像的映射位置f(v)
			int m=(int)(t.x);
			int n=(int)(t.y);
			m-=Orig_x;
            n-=Orig_y;
			color=cvGet2D(pImage,i,j);//像素获取
			if(0<=m && dImage->width>m && 0<=n && dImage->height>n)
			{
			cvSet2D(dImage,n,m,color);
			}
		}
	}

图像变形算法，有正向映射和逆向映射，如果按照每个像素点，都通过上面的计算方法求取其对应变换后的像素点位置，那么其实计算量是非常大的，因为一幅图像的像素点，实在是太多了，如果每个像素点，都用上面的函数遍历过一遍，那计算量可想而知。

因此一般的变形算法是对待图像进行三角剖分：

然后只根据只对三角网格模型的顶点，根据变形算法，计算出三角网格模型每个顶点的新位置，最后再用三角形仿射变换的方法，计算三角形内每个像素点的值，得到变形后的图像，这样不仅速度快，同事解决了正向映射与逆向映射变形算法存在的不足之处，具体图像变形的正向和逆向映射存在的缺陷，可以自己查看相关的文献。

另外两种相似变换和刚性变换，可以自己查看M矩阵的计算公式，编写实现相关代码。

本文地址：http://blog.csdn.net/hjimce/article/details/46550001     作者：hjimce     联系qq：1393852684   更多资源请关注我的博客：http://blog.csdn.net/hjimce                原创文章，版权所有，转载请保留本行信息。

参考文献：

1、《Image Deformation Using Moving Least Squares》

2、《3D Deformation Using Moving Least Squares》