算法入门4:动态规划
分治算法将规模较大的问题划分成规模较小的子问题,通常,这些子问题是不重叠的。
这一篇要介绍的动态规划算法,也是基于问题划分,区别在于划分的子问题是有重叠的(黄色部分),这样在求解的过程中,对于重叠的部分只要求解一次,记录下结果(备忘录方法),其他子问题中直接使用即可,减少了重复计算,效率更高。
如下图,在计算子问题A的时候需要计算A的子问题a,b,c,计算B的时候需要计算b,c,d,这里b,c就是重叠部分。按照分治算法,b,c需要分别计算两次。按照动态规划,b,c只要求解A时计算一次,然后记录结果,在求解B时,直接使用。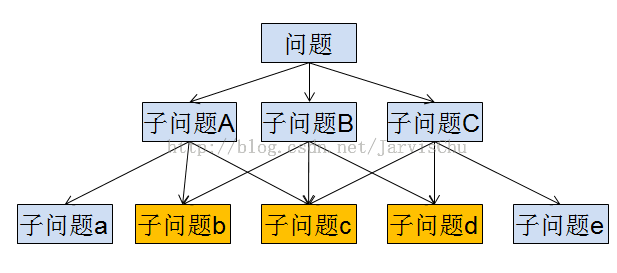
动态规划算法常用于求解最优解问题。
动态规划算法
所谓动态规划,其动态就表现在求解一个问题最优解时,不是固定的计算、合并某些子问题的解,而是根据各子问题的解的情况,选择其中最优的。
例如:DP(n) = max{ DP(n-1)+1, DP(n-2)+2 }
求解规模为n的问题的解,等于DP(n-1)+1 和 DP(n-2)+1中的较大的值
简单理解动态规划,就是解当前问题的最优解时,综合考虑从其各子问题的最优解,从中构成得到当前问题的最优解。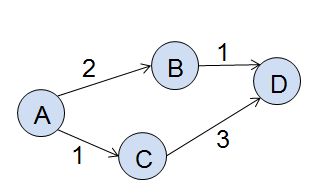
比如要计算从A到D的最短路径DP(A),其子问题为DP(B)和DP(C)。那么
其中AB = 2,AC=1
可见,在A处,不是简单考虑当前,认为AC<AB,所以走AC,然后走到C时,再作A类似的思考(这其实是贪心算法的思想)。而是,考虑B、C到D的距离,即DP(B)和DP(C),再结合AB、AC做出选择,这就是动态规划(长远眼光:))。
动态规划的要素
显然,不是所有问题都能(或需要)使用动态规划算法求解。一个问题如果需要用动态规划算法求解,它需要具有如下两个性质(要素):
- 最优子结构性质
- 子问题重叠性质
最优子结构性质
问题的最优解包含了其子问题的最优解,这种性质称为最优子结构性质
怎么理解这个性质?
该性质是指问题的最优解,是由其子问题的最优解构成,但具体是怎么构成的?不是简单的自下而上,诸如由DP(n-1)的最优解得到DP(n)的最优解之类,而是DP(n)的最优解可能由DP(n-1)构成,也可能和DP(n-1)没有关系,而是由DP(n-2)的最优解构成。这就是定义里用的是包含的意思。
再详细的,后面结合例子再具体讲解。
子问题重叠性质
这也是动态规划算法的一个关键。
动态规划算法其实是一种自下而上的算法,先计算出子问题的解,再由子问题的解去构造问题的解。
由于子问题存在有重叠,所以可以通过备忘录的方法,把子问题的最优解记录下来,当再次用到时,直接从备忘录中读取即可,不必再次使用,这就提高效率。
动态规划的步骤
包括如下4个步骤:
1. 描述最优解的结构
2. 递归定义最优解的值
3. 按自底向上的方式计算最优解的值
4. 由最优解的值构造一个最优解
最优解的值指的是:求解得到的问题的最优的值,如最大值,最小值;
最优解指的是:得到最优的值时所用的具体方法,如背包问题中具体怎么放置物品;
经典问题
(1)装配线调度
(2)矩阵连乘
(3)最长公共子序列
(4)背包问题
(5)多边形游戏
(6)最优三角剖分
(7)最优排序二叉树
(8)最优合并问题
最长公共子序列
问题
若给定序列X={x1,x2,…,xm},则另一序列Z={z1,z2,…,zk},是X的子序列是指存在一个严格递增下标序列{i1,i2,…,ik}使得对于所有j=1,2,…,k有:zj=xij。例如,序列Z={B,C,D,B}是序列X={A,B,C,B,D,A,B}的子序列,相应的递增下标序列为{2,3,5,7}。
给定2个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。
给定2个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn},找出X和Y的最长公共子序列。
分析
序列X和Y使用数组表示:X[1…N],Y[1…N],使用二维数组Z[N+1][M+1]定义解,其中Z[i][j] 表示 {X1,...,Xi}与{Y1,...,Yj}的最长公共子序列长度。如:Z[1][2]表示 {X1} 与 {Y1,Y2}
由上面的定义可知:
Z[i][0] 表示X{…} 与 空序列Y {} 的公共子序列,故Z[i][0] = 0
Z[0][j] 表示空序列X {}{} 与Y {…} 的公共子序列,故Z[0][j]= 0
递推公式如下: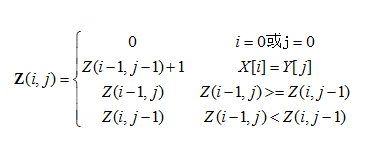
为了求得最长公共子序列的具体值,需要在求解公共子序列长度的时候,添加标志(或称为备忘)以记录求解过程的每一步,便于在得到长度后,回溯求解过程,得到具体的序列。
下面的代码中使用how[N+1][M+1] 完成这一功能。
代码:
/************************************************************************
* 名 称:LCS.cpp
* 功 能:动态规划算法案例:最长公共子序列
* 作 者:JarvisChu
* 时 间:2013-11-8
************************************************************************/
#include <iostream>
#define N 8
#define M 7
char X[N+1]={' ','A','B','C','D','E','F','G','H'};// 序列 X X0不用
char Y[M+1]={' ','B','D','G','H','A','F','A'}; // 序列 Y Y0不用
//#define N 4
//#define M 3
//char X[N+1]={' ','A','B','C','D'};// 序列 X X0不用
//char Y[M+1]={' ','A','B','D'}; // 序列 Y Y0不用
int Z[N+1][M+1]; //Z[i][j] 表示 {X1,...,Xi}与{Y1,...,Yj}的最长公共子序列长度
//Z[0][0] 表示 {} 与 {}
//Z[1][2] 表示 {X1} 与 {Y1,Y2}
int how[N+1][M+1]; //记录最长公子序列是如何得到的,用来追溯Z,得到具体的公共子序列
//how[i][j] = 0 表明记录 Z[i][j] = Z[i-1][j-1]+1, X[i] == Y[j] 时;
//how[i][j] = 1 表明记录 Z[i][j] = Z[i-1][j], X[i] != Y[j] 时;
//how[i][j] = 2 表明记录 Z[i][j] = Z[i][j-1], X[i] != Y[j] 时;
/*----------------------------------------------------------------------------------
* 功 能: 求序列 X和Y的最长公共子序列的长度 [求最优解的值]
* 参 数:
* 返 回:无
------------------------------------------------------------------------------------*/
void LCSLength()
{
int i,j;
//X的{} 和 Y的{}{Y1}...{Y1,Y2}的公共子序列长度为0;同理有Y的{}
for(i=0;i<N;i++) Z[i][0] = 0;
for(j=0;j<M;j++) Z[0][j] = 0;
//考虑其他情况,X和Y都顺序增长
for(i=1;i<=N;i++)
{
for(j=1;j<=M;j++)
{
//X,Y当前元素相等,公共子序列长度加1
if(X[i] == Y[j])
{
Z[i][j] = Z[i-1][j-1]+1;
how[i][j] = 0;
}
//Z[i][j] = max(Z[i-1][j],Z[i][j-1]);
else if(Z[i-1][j] >= Z[i][j-1])
{
Z[i][j] = Z[i-1][j];
how[i][j] = 1;
}
else
{
Z[i][j] = Z[i][j-1];
how[i][j] = 2;
}
}
}
}
/*----------------------------------------------------------------------------------
* 功 能: 追溯Z,得到具体的公共子序列 [求最优解]
* 参 数:
* 返 回:无
------------------------------------------------------------------------------------*/
void LCS(int i,int j)
{
if(i==0 || j==0) return ;
if(how[i][j] == 0)
{
LCS(i-1,j-1);
std::cout<<X[i]<<" ";
}
else if(how[i][j] == 1)
{
LCS(i-1,j);
}
else
{
LCS(i,j-1);
}
}
int main()
{
//最长公共子序列的长度
LCSLength();
std::cout<<Z[N][M]<<std::endl;//长度
//for(int i=0;i<=N;i++)
//{
// for(int j=0;j<=M;j++)
// {
// std::cout<<Z[i][j]<<" ";
// }
// std::cout<<std::endl;
//}
LCS(N,M);
return 0;
}
转载本文请注明作者和出处
作者 :JarvisChu
出处:http://blog.csdn.net/jarvischu
