数据结构之树与二叉树
原来学C++的时学过树和二叉树的一些知识,其实当时学的挺模糊,正好这次又有这个机会,所以在此总结一下树和二叉树。文章脉络如下图:
树的基本概念
在说其它之前得先说说树的一些概念定义。
结点的度为:该结点的下结点的个数;
树的度:最大结点的度;
叶子节点:没有子节点的结点;
分支结点:除了叶子节点其它全部为分支结点;
内部结点:除了根节点和叶子节点的结点;
父节点、子节点、兄弟结点为相对概念,不能单独存在,可以说5号结点是2号结点的子节点,2和3是兄弟结点;
树的遍历
是指查看树所有的结点。
按照遍历父节点、左子结点和右子结点的先后顺序不同,可以分为前序遍历、层次遍历和后序遍历。遍历的共同之处在于,都是递归执行。遍历的命名可以根据父节点的访问顺序而得知,例如前序遍历是最先遍历父节点等。
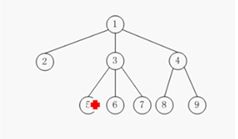
以下图为例,说明三种遍历方式:
前序遍历:按照先父结点后子结点(自左向右)的顺序遍历树的所有结点。树的第一个父节点为根节点即上图中的结点1;然后是1的子结点2;因为结点2下面还有结点,按照递归的方法,应该继续遍历2的子节点5;5没有子节点,然后自左向右遍历结点:依次为6、7;2的子节点遍历完毕后是结点3;3没有子节点所以自左向右遍历结点4;通向遍历结点8;遍历8的子节点9和10;遍历结束,得到的最终结果为1、2、5、6、7、3、4、8、9、10。
后序遍历:按照先子节点后父节点、自左向右的顺序遍历树的所有结点。继续使用上图,树的最左的一个子结点为5,所以从5开始,依次为5、6、7;然后是它们的父节点2;按照自左向右的原则,结点2的兄弟节点有3和4;但是因为4有子节点8和8有子节点9 和10;故先从9、10遍历;得到的后序遍历结果为5、6、7、2、3、9、10、8、4、1。
层次遍历:这种遍历方式非常简单,最符合日常逻辑:自上而下、自左向右依次遍历结点,所以得到的结果为:1、2、3、4、5、6、7、8、9、10。
树和二叉树的转换
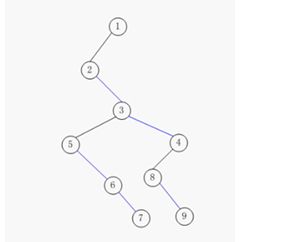
转换法则很简单:树的最左子树转换为二叉树的左子树,其它兄弟结点为此左子结点的子节点。如下图:
2为原树的最左子节点,在二叉树中为根节点1的子节点,3、4与2为兄弟结点,在二叉树中转换为2的子节点,自上向下,逐级转化可以得到:
调整结点位置得到:
有木有想过为什么要转化?个人认为是树虽然更接近实际的存储但是实际操作复杂,二叉树更接近计算机的思维,且二叉树有更多的规则更容易制定和使用。
二叉树
二叉树概念
顾名思义,二叉树每个树枝上有最多两个叉,个人意见。
二叉树的特性
1. 第i层(树从0层开始)最多有2i-1个结点
2. 深度为i的树最多有2i-1个结点
3. 如果其叶子结点数目为n0,度为2的结点树为n2,则n0=n2+1
4. 具有n个结点的完全二叉树的深度为x+1(x为不大于log2n的最大整数)
5. 一棵二叉树的前序遍历和中序遍历可以唯一确定这棵二叉树
二叉树的遍历
二叉树的遍历和树的遍历类似,只是多了一个中序遍历。以下图为例
中序遍历:按照左子节点--根节点--右子结点、自左向右遍历树
满二叉树
一颗深度为k的二叉树,它有2k-1个结点,则称之为满二叉树。
完全二叉树
深度为k,有n个结点的二叉树,其结点能够与深度为k的满二叉树从1到n相对应。
查找二叉树
根节点若非空,左子结点<父节点<右结点。
注意二叉树中没有相同数值的结点,插入结点时根据大小值选择插入地方。从其命名也可以看出来,这样的排序,想要查找或比较某一个值,根据这个树的特性较为容易,有点类似二分法查找:先比较父节点,根据结果可以知道,下一步要比较的是左子树还是右子树。
静态查找:在树结构中查找键值为k的结点。
1. 如果二叉树为空,查找失败,结束查找
2. 如果根结点值为k,查找成功,结束查找
3. 如果k小于根结点值,则沿左子树查找,如果k大于根结点值,则沿右子树查找
动态查找:为插入和删除而是用的查找,动态查找得到两个指针:一个指向键值为key的结点,另一个指向该结 点的父结点。
插入结点:利用动态查找确定新结点的位置分下列情况对待:
• 已有相同键值的结点存在,则不再插入
• 如果二叉树为空二叉树,则以新节点为查找二叉树。
• 将要插入的结点值与插入后的父结点值比较,依此确定为父节点的左子结点还是右子结点
删除结点
在查找二叉树上删除一个节点时,要考虑三种情况:
①若待删除的节点p是叶子节点,则直接删除该节点;
②若待删除的节点p只有一个子节点,则将这个子节点与待删除节点的父节点直接连接,然后删除节点p;
③若待删除的节点p有两个子节点,则在其左子树上,用中序遍历寻找关键值最大的节点s,用节点s的值代替节 点p的值,然后删除节点s,节点s必属于上述①,②情况之一。
最优二叉树
先了解一下这些概念:
路径长度:从根节点到目标结点的路径长度
权:即结点的值
带权路径长度:路径长度乘以其自身的值
树的代价:所有结点值与自身树的路径乘积之和
哈夫曼树:即为树的代价最小的树
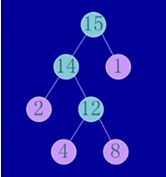
例如把下面的树,转换为最优二叉树:
得到
先不说怎么转换,先看看这棵树的特点:权值大的里根节点越近,权值越小离根节点越远,正是这样才能保证权值乘以路径的和才能最小。个人认为转换步骤的原则就是越小的离跟几点越远。
根据哈夫曼树可以推出哈夫曼编码,在此就不介绍了。
线索二叉树
为什么会有线索二叉树,因为普通二叉树会有多个指针为空:设有n个结点,只是用了n-1个指针,另外n+1个指针为空。线索二叉树就是为了充分利用这些空指针而产生的。
在线索二叉树中,结点的表示为:
| Lbit |
Lchild |
Data |
Rchild |
Rbit |
增加最左和最右这两个标志的作用是:当Lbit为0时,指向的是左子结点;当Lbit为1时,指向的是前驱结点,Rbit作用相同。
平衡二叉树
平衡二叉树的前提是查找二叉树,是为了保证二叉树的高度为log2n,从而保证查找二叉树插入、删除、查找的平均时间为log2n。平衡二叉树的任一结点的左子结点、右子结点高度之差绝对值不超过1。
这里更着重介绍了这些树的区别和联系,关于树的复杂操作正在学习中。