海量数据挖掘MMDS week2: Association Rules关联规则与频繁项集挖掘

http://blog.csdn.net/pipisorry/article/details/48894977

海量数据挖掘Mining Massive Datasets(MMDs) -Jure Leskovec courses学习笔记之association rules关联规则与频繁项集挖掘

{Frequent Itemsets: Often called "association rules," learn a number of techniques for finding items that appear unusually often together.  The classical story of "beer and diapers" (people who buy diapers in a supermarket are unusually likely to buy beer) is an example of this data-mining technique.}

题外话: lz真的不建议看这个视频，当你看了这个视频后，你会发现，原本一个简单的问题可以通过很优雅的方式简单地解释清楚的时候，主讲人总是偏离方向，以一种相当繁琐隐晦的形式讲到另一个地方去，而让人一下子就可以明白的解释总是讲不出来，让人看不懂（说真的，那个比较老的主讲人讲解的是相当水），并且制作的ppt中的语句完全不是最好的，总是缺点什么，总要加一点注释在下面才能更好明白那是什么意思。所以关于频繁项集挖掘以及关联规则，lz建议看看《数据挖掘概念与技术》这本书中第六章 挖掘频繁模式、关联和相关性：基本概念与方法的内容，讲的相当清晰易懂）

Frequent Itemsets频繁项集

与相似性分析的区别：相似性分析，研究的对象是集合之间的相似性关系。而频繁项集分析，研究的集合间重复性高的元素子集。

Market-Basket 模型及其应用

Note: 一个item可以看成是买的一个东西，其集合就是项集。一个basket就是买的东西的集合，也是一个项集，但一般看作是多个项集的集合。

频繁项集的应用：真实超市购物篮的分析，文档或网页的关联程序分析，文档的抄袭分析，生物标志物（疾病与某人生物生理信息的关系）

应用一：人们会同时买什么

Note:

1. Run a sale on diapers; raise price of beer.是一种营销策略，但是反过来却不是。这就要分析频繁项集的原因。

2. 当然这种营销策略只对实体店有效。超市购物篮的分析，主要是针对实体销售商，而不是在线零售商，这是因为实体销售可以找点频繁项集合后，可以采取对一种频繁项商品促销，而抬高相关的频繁项其他商品的价格来获利，因为客户一般不会去另外一家店购买其他的商品。而这种策略在在线销售时，会忽略“长尾”客户的需求。对于实体销售，商品的数量和空间资源有限，所以只能针对一些畅销商品进行关注和指定策略。而对于在线销售，没有资源限制，而且客户切换商户很方便，所以实体店销售的策略不合适在线销售，在线销售更应该关注相似客户群的分析，虽然他们的购买的产品不是最畅销、频繁的，但对客户群的偏好分析，可以很容易做到对每个客户进行定制化广告推荐，所以，相似性分析对在线销售更为重要。

应用二：抄袭plagiarism检测

Note: the basket corresponding to a sentence contains all the documents in which that sentence appears.
应用三：词关联

关联规则Association Rules、支持度与置信度

Support支持度

 

支持度： 包含频繁项集F的集合的数目。项集的支持度就是项集应该在所有basket中出现的数目。>=项集的支持度的项集都是频繁项集。

Confidence置信度

  

置信度：confidence(A=>B) = P(B|A) = support(A U B)/support(A) = support_count(A U B)/support_count(A)，就是itemA存在时itemB也存在的条件概率，也是频繁项A与某项B的并集的支持度 与 频繁项集A的支持度的比值。

寻找关联规则和频繁项集

关联规则挖掘两个步骤

1. 寻找所有频繁项集（满足最小支持度的项集）

2. 由频繁项集产生关联规则（满足最小支持度和最小可信度的项集）

Note: 确定频繁项集，{i}只需要support，而{i,j}则需要support*confidence.

Note:

1. 这种寻找关联规则的方法步骤是：先找到支持度>=cs的，然后去掉其中一个item j，找到支持度>=s的，这样去掉j后的项集{i}->j的置信度>=c，{i}->j就是一个关联规则。

2. 这种解释完全没有《数据挖掘概念与技术》中的解释清晰明了。

频繁项集的计算模型

算法瓶颈

寻找频繁二项集的算法

Naive Algorithm朴素算法

关联规则的整体性能有第一步决定，给定n项，可能有2的n次方个候选项。当然这个算法不是很有效，后面会用Apriori算法代替。

频繁项对{i, j}在内存中的存放方式

{用什么数据结构来存储频繁二项集数对更有效}

 

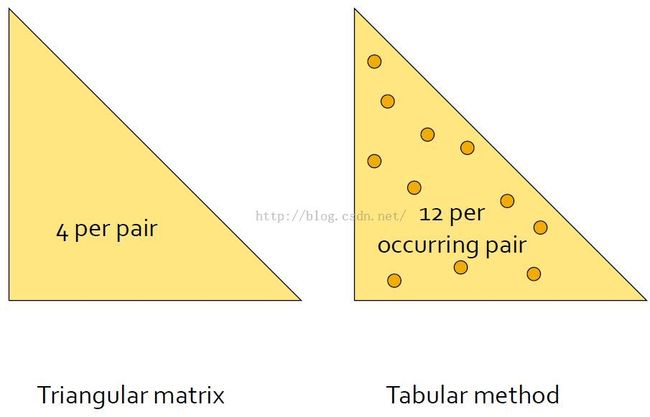
Triangular Matrix三角阵方法

{采用一个数组来存储这个三角阵中的元素，它可以节省二维数组一半的空间}

Note: translate from an items name in the data to its integer.A hash table whose key is the original name of the item in the data will do just fine.

Note: 因为pairs存放在一个一维数组中。则频繁对(i, j)存放的位置就是上面这个公式。

Tabular三元组方法

{当频繁项对的数目小于C(n, 2)的数目的1/3时，三元组的方式相对于三角阵比较有优势}

Note: 链表实现需要指针指向下一个，这样就是16p而不是12p了。

两种方法的比较和取舍

如果有大于1/3的候选二项集是频繁二项集，那么使用Triangular结构存储比较好。if more than one-third of possible pairs are present in at least one basket,you prefer the triangular matrix.

设频繁一项集数目为N，频繁二项集的数目为M，候选二项集自然就是N^2/2。则使用Triangular矩阵存储频繁二项集的空间为4*N^2/2， 使用Tabular结构存储频繁二项集的空间为12*M。当大于1/3的候选二项集是频繁二项集，也就是1/3 * N^2/2 < M，这时4*N^2/2 < 12*M，使用Triangular矩阵存储频繁二项集的空间较小。

皮皮blog

A-priori算法

{通过限制候选产生来发现频繁项集。Aprior有点类似广度优先的算法。}

频繁项集的先验性质：单调性和反单调性

Note: 寻找频繁二项集是扫描两次，频繁k项集当然是k次。if you want to go pass pairs to larger item sets,then you need k passes, define frequent items that's of size up to K.

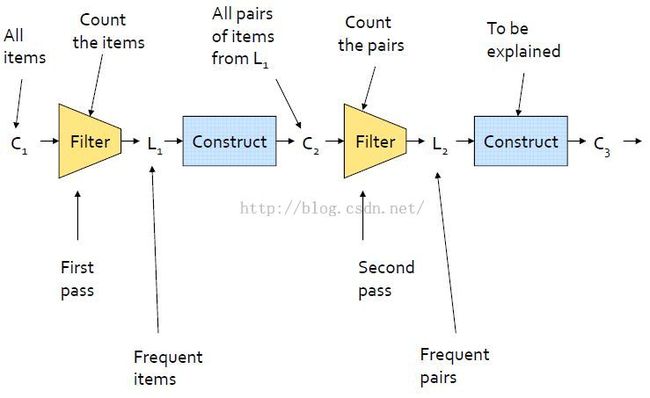
A-priori算法步骤

频繁二项集的挖掘

  

If there's still too many counts to maintain in main memory,we need to try something else,a different algorithm,splitting the task among different processors, or even buying more memory.

A-Priori算法中使用Triangular Matrix

  

Note:

1. 也就是第一次扫描后，选出频繁一项集并重新编号，组成Triangular Matrix。在Triangular Matrix中再选出频繁二项集重新编号，并组成Triangular Matrix，再进行下一次Apriori算法的计算。

2. There are better ways to organize the table that save space,if the fraction of items that are frequent is small.For example, we could use a hash table in which we stored only the frequent items with the key being the old number and the associated value being the new number.(也就是Tabular?)

频繁K项集挖掘

 

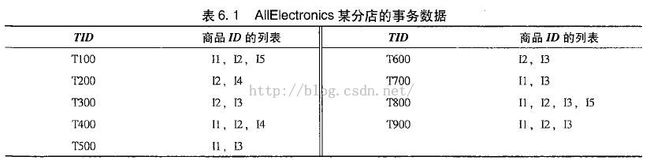
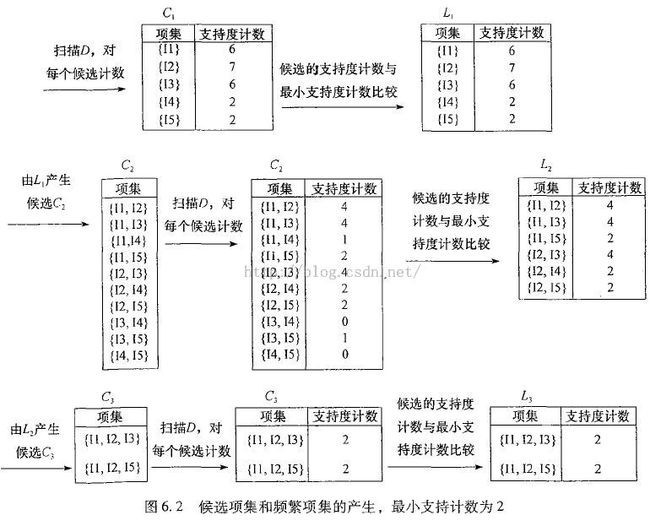
数据挖掘概念与技术中对Apriori算法的图解

数据挖掘概念与技术中对Apriori算法的描述

是不是简单清晰得多！

Apriori算法内存需求分析

每次计算一个频繁k{k = 1-K}项集，都要扫描一次basket(transaction交易)

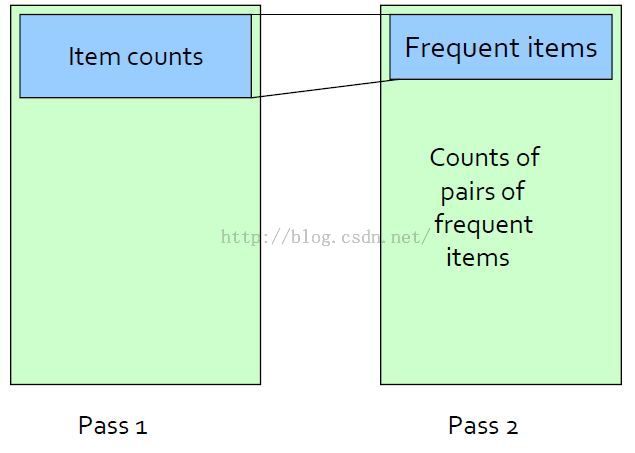
Apriori算法的内存的使用情况，左边为第一步时的内存情况，右图为第二步时内存的使用情况

在第一步（对所有item扫描计数，并选出频繁一项集）里，我们只需要两个表，一个用来保存项的名字到一个整数的映射，用这些整数值代表项，一个数组来计数这些整数。

皮皮blog

Reviews复习

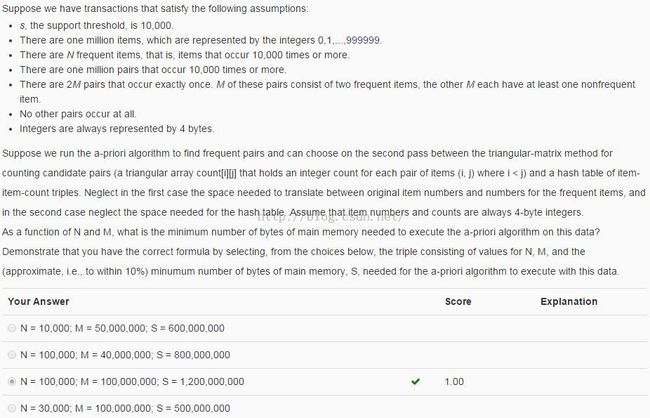
Triangular Matrix和Tabular的选择

Note: S是N和M的函数。

从上面分析可知：如果有大于1/3的候选二项集是频繁二项集（也就是1/3 * N^2/2 < M <=> N^2 < 6M），那么使用Triangular结构存储比较好。并且使用Triangular矩阵存储频繁二项集的空间为4*N^2/2， 使用Tabular结构存储频繁二项集的空间为12*M。

N = 10,000, M=50,000,000,则N^2 = 10^8 < 6M=3*10^8,故使用Triangular矩阵来存储频繁二项集，空间为S = 4*N^2/2=2*10^8。(的确比12*M = 6*10^8小)

N = 100,000, M=40,000,000,则N^2 = 10^10 > 6M=2.4*10^8,故使用Tabular来存储频繁二项集，空间为S =12*M=4.8*10^8。(的确比4*N^2/2= 2*10^10小)

N = 100,000, M=100,000,000,则N^2 = 10^10 > 6M=6*10^8,故使用Tabular矩阵来存储频繁二项集，空间为S =12*M=12*10^8。(的确比4*N^2/2= 2*10^10小)

N = 30,000, M=100,000,000,则N^2 = 9*10^8 > 6M=6*10^8,故使用Tabular矩阵来存储频繁二项集，空间为S =12*M=18*10^8。(的确比4*N^2/2= 12*10^8小)

from:http://blog.csdn.net/pipisorry/article/details/48894977