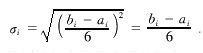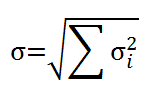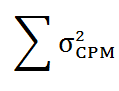项目管理知识笔记四:PERT值计算
PERT的计算特点
PERT首先是建立在网络计划基础之上的,其次是工程项目中各个工序的工作时间不肯定,过去通常对这种计划只是估计一个时间,到底完成任务的把握有多大,决策者心中无数,工作处于一种被动状态。在工程实践中,由于人们对事物的认识受到客观条件的制约,通常在PERT中引入概率计算方法,由于组成网络计划的各项工作可变因素多,不具备一定的时间消耗统计资料,因而不能确定出一个肯定的单一的时间值。
在PERT中,假设各项工作的持续时间服从β分布,近似地用三时估计法估算出三个时间值,即最短、最长和最可能持续时间,再加权平均算出一个期望值作为工作的持续时间。在编制PERT网络计划时,把风险因素引入到PERT中,人们不得不考虑按PERT网络计划在指定的工期下,完成工程任务的可能性有多大,即计划的成功概率,即计划的可靠度,这就必须对工程计划进行风险估计。
在绘制网络图时必须将非肯定型转化为肯定型,把三时估计变为单一时间估计,其计算公式为:
式中:
- ti为i工作的平均持续时间(PERT值);
- ai为i工作最短持续时间(亦称最乐观估计时间);
- bi为i工作最长持续时间(亦称最悲观估计时间);
- ci为i工作正常持续时间(最可能时间),可由施工定额估算。
其中,ai和bi两种工作的持续时间一般由统计方法进行估算。
三时估算法把非肯定型问题转化为肯定型问题来计算,用概率论的观点分析,其偏差仍不可避免,但趋向总是有明显的参考价值,当然,这并不排斥每个估计都尽可能做到可能精确的程度。为了进行时间的偏差分析(即分布的离散程度),可用方差估算:
式中:σ2i为i工作的方差。
标准差
活动历时在[PERT-σ,PERT+σ]区间的概率为68.26%
所以有结论是:
1σ=68.26%
2σ=95.43%
3σ=99.73%
6σ=99.99966%
一般计算步骤如下:
1).每个活动有三个值,最可能时间,最悲观时间,最乐观时间
2).计算每个活动的pert值
3).计算每个活动的方差
4).画活动网络图,一般是前导图
5).找出关键路径,
6.)计算项目的pert值,即关键路径的pert 值之和
计算项目的σ,
项目的σ=项目方差的平方根
项目方差=各个活动的方差之和
7)计算区间概率,
例如: 项目在[pert-σ,pert+σ]期间完成的概率为68.26%
例题:
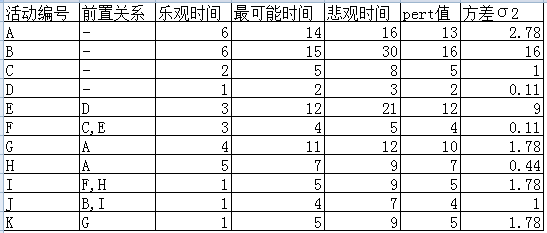
有如下一个项目活动,
问题:
1)此项目关键路径是什么?
2)此项目在什么日期内完成的概率能达到95%?
答案:
1)画前导图,图略
得出关键路径是A ,H ,I ,J
2) 关键路径上的Pert值 是 13,7,5,4
项目Pert值=13+7+5+4=29 天
项目的方差=
=2.78+0.44+1.78+1=6
项目的σ=6^0.5=2.45
95%的概率区间为[Pert-2σ,Pert+2σ] ,即[29-2*2.45,29+2*2.45]时间内完成概率为95% ,[24.1,33.9]天内完成概率为95%。
三角分布的计算方法:
Te=(O+ M+P)/3
Te为平均持续时间(PERT值);
O 为工作最短持续时间(亦称最乐观估计时间);
P 为工作最长持续时间(亦称最悲观估计时间);
M为工作正常持续时间(最可能时间)。