动态规划入门(四)DP 基本思想 具体实现 经典题目 POJ1160 POJ1037
POJ1160, post office。动态规划的经典题目。呃,又是经典题目,DP部分的经典题目怎就这么多。木有办法,事实就这样。
求:在村庄内建邮局,要使村庄到邮局的距离和最小。
设有m个村庄,分别为 V1 V2 V3 … Vm, 要建n个邮局,分别为P1 P2 P3 … Pn。
在DP的问题中,经常有从m个物体中选n个物体的情况,本题显然也属于这种情况。一般可以这样考虑:假设已经选了1个,那么就成了在m-1个中选n-1个的问题了。
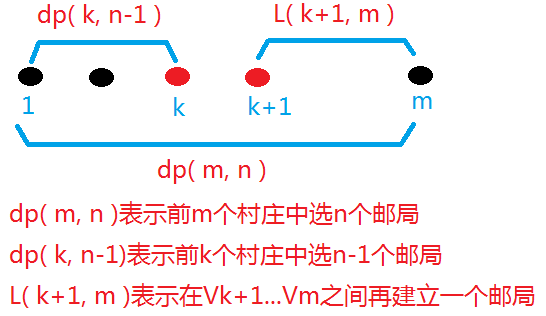
对于此题,也可以考虑先建一个邮局。建在哪里呢?不妨设,该邮局建在Vk+1..Vm之间的某个村庄里,而且规定Vk+1..Vm之间再不允许建立其他邮局了。因此,剩下的n-1个邮局必然出现在V1..Vk之间的村庄内,这样问题就转换成:在前k个村庄里选n-1个邮局的问题。
设dp( m,n )表示在V1…Vm之间建立n个邮局时的最短距离。
L( i, j )表示在Vi…Vj之间建立一个邮局的最短距离。
状态转换方程:
dp( m,n ) = Min( dp( k,n-1 ) + L( k+1,m ) ), 其中:1 <= k<m
编程实现:没啥说的,具体看代码。
POJ1037, a decorative fence。这个题绝对不是入门级的,如果能独立做出来,那已经很NB了。嘿嘿,这一大段英文,先要把题目看懂就得费些气力。
问题:有n个长度不同的木条,现在按照类似字典顺序(长度小的排在前)对这n个木条排序,求第m个图像是什么?
设这n个木条分别为S1 S2 S3…Sn,它们的对应长度分别为1 2 3...n.
对这n个木条进行排序,结果无非有下面n类: 以S1开头,以S2开头…以Sn开头。按照题目要求对这n类进行排序。
S1 。。。
S2 。。。
。。。
Sn 。。。
如果能算出每个区间有多少种排列,那么就能确定要求的第m个排列了。好抽象呀,还是举个例子吧。如果以S1开头的有10种排列,以S2开头的有10种排列…现在有n个木条,如果要确定第15个排列,那么就可以知道第15个排列必然是以S2开头的。因为已经知道了最终排列的第一个木条是S2,那么只要依次求出后面n-1个木条即可。如果能把S2开头的区间再划分成若干个区间,并且知道每个区间的大小就和上面的问题一样了。
S2 S1 。。。
S2 S3 。。。
。。。
S2 Sn 。。。
这时问题就转换为:有n-1个木条,现在要确定第5个排列(15-10=5,以S1开头的排列已占去了10个)
现在结合题目,题目要求出现波浪形,即有高度变换。这时以Si开头的排列又可以分成两类:第二个木条比Si高,我们记做Hi, 第二个木条比Si低,我们记做Li。这时区间细分成如下形式:
L1 。。。
H1 。。。
L2 。。。
H2 。。。
。。。。。。
Ln 。。。
Hn 。。。
要确定最终的排列,关键是要知道每个区间里排列的个数。
设L( x,n )表示n个木条的排列中,以长度为x的木条开始,且下一个木条比X低的排列数。H( x,n )表示n个木条的排列中,以长度为x的木条开始,且下一个比X高的的排列数
状态转换方程:
L( x, n ) = , 其中 1 <= i < x
H( y, n ) = , 其中 y <= i < n
有状态方程在手,就可以依次确定要求排列的每个木条。
参考资料:
http://jay23jack.blog.163.com/blog/static/317951942009130215813/
http://blog.163.com/leyni@126/blog/static/16223010220103150173663/
POJ1160
#include <iostream>
using namespace std;
//***********************常量定义*****************************
const int V_MAX = 305;
const int P_MAX = 35;
const int INF = 999999999;
//*********************自定义数据结构*************************
//********************题目描述中的变量************************
//村庄数
int vNum;
//邮局数
int pNum;
//村庄坐标
int vPos[V_MAX];
//**********************算法中的变量**************************
//d[i][j]表示在村庄i和村庄j之间建1个Post office的最小距离和
int d[V_MAX][V_MAX];
//dp[i][j]表示在村庄1和村庄i之间建j个Post office的最小距离和
int dp[V_MAX][P_MAX];
//***********************算法实现*****************************
void Solve()
{
int i, j, k;
//利用DP,计算d[i][j]的值
for( i=1; i<=vNum; i++ )
{
for( j=i+1; j<=vNum; j++ )
{
d[i][j] = d[i][j-1] + ( vPos[j] - vPos[( i + j )/2] );
}
}
for( i=1; i<=vNum; i++ )
{
dp[i][0] = INF;
}
//利用DP,计算dp[i][j]的值
for( i=1; i<=vNum; i++ )
{
for( j=1; j<=pNum && j<=i; j++ )
{
int min = INF;
for( k=j-1; k<i; k++ )
{
if( dp[k][j-1] + d[k+1][i] < min )
min = dp[k][j-1] + d[k+1][i];
}
dp[i][j] = min;
}
}
cout << dp[vNum][pNum] << endl;
}
//************************main函数****************************
int main()
{
//freopen( "in.txt", "r", stdin );
cin >> vNum >> pNum;
for( int i=1; i<=vNum; i++ )
{
cin >> vPos[i];
}
Solve();
return 0;
}
POJ1037
#include <iostream>
using namespace std;
//***********************常量定义*****************************
const int MAX_N = 25;
//*********************自定义数据结构*************************
//********************题目描述中的变量************************
//木条的数目
int n;
//栅栏的编号
long long c;
//**********************算法中的变量**************************
//up[n][i]表示:n个木条,且第一个木条长度为i的上升型栅栏数目
long long up[MAX_N][MAX_N];
//down[n][i]表示:n个木条,且第一个木条长度为i的下降型栅栏数目
long long down[MAX_N][MAX_N];
bool used[MAX_N];
bool isPrint;
//***********************算法实现*****************************
void FillTable()
{
down[1][1] = 1;
up[1][1] = 1;
down[2][1] = 0;
up[2][1] = 1;
down[2][2] = 1;
up[2][2] = 0;
int i, j, k;
for( i=3; i<MAX_N; i++ )
{
//??? j<=MAX_N
for( j=1; j<MAX_N; j++ )
{
//??? k=j
for( k=j; k<i; k++ )
{
up[i][j] += down[i-1][k];
}
for( k=1; k<j; k++ )
{
down[i][j] += up[i-1][k];
}
}
}
}
void SolveAndPrint( int id, int count )
{
for( int i=1; i<=count; i++ )
{
if( used[i] && i<=id )
{
id++;
count++;
}
}
used[id] = true;
if( isPrint )
{
cout << " " << id;
}
else
{
cout << id;
isPrint = true;
}
}
//************************main函数****************************
int main()
{
//freopen( "in.txt", "r", stdin );
int caseNum;
cin >> caseNum;
//DP的填表
FillTable();
while( caseNum-- )
{
cin >> n >> c;
//先搜索down
bool isDown = true;
bool isFirst = true;
int id = 1;
isPrint = false;
memset( used, 0, sizeof(used) );
while( n )
{
if( isDown )
{
if( c > down[n][id] )
{
c -= down[n][id++];
if( isFirst )
{
//设置标记,下次搜索up
isDown = false;
//对每个id有down和up两个值
//确定第一个数时,down和up都要搜索
id--;
}
}
else
{
//如果当前木条长度可确定
//问题规模减一
SolveAndPrint( id, n-- );
isFirst = false;
isDown = false;
id = 1;
}
}
else
{
if( c > up[n][id] )
{
c -= up[n][id++];
if( isFirst ) isDown = true;
}
else
{
SolveAndPrint( id, n-- );
isFirst = false;
isDown = true;
}
}
}
cout << endl;
}
return 0;
}