【模式匹配】之 —— Z-BOX算法
- 一 Z-BOX的概念
- 二 Z-BOX算法的计算过程
- 三 Z-BOX算法的代码实现C语言版
- 四 Z-BOX算法在具体的模式匹配字符串查找中的应用
- 五 总结
- Z-BOX算法
- KMP算法
- BM算法
- sunday算法
第一篇文章,我们从Z-BOX算法开始讲起,因为Z-BOX算法的思想可以做为KMP算法和BM算法中求子串匹配过程的基础。
一 Z-BOX的概念
对于一个模式串P,记为a0,a1,a2...an。
Zi(P)的值表示,从下标i开始的子串,能够和从P开头的子串进行匹配的长度。
举例说明,例如模式串P = aabaaabd
下标:01234567
那么对应的Zi(P)值如下:
| i | Zi(p)值 | 说明 |
| 0 | 略过 | |
| 1 | 1 | p[1] = p[0] |
| 2 | 0 | p[2] != p[0] |
| 3 | 2 | p[3, 4] = p[0, 1] |
| 4 | 3 | p[4,5,6] = p[0,1,2] |
| 5 | 1 | p[5] = p[0] |
| 6 | 0 | p[6] != p[0] |
| 7 | 0 | p[7] != p[0] |
之所以称为Z-BOX,是因为能够匹配上的子串,像一个盒子一样,例如上例中的Z4(P) = 3,也就是从P[4]开始有3个字符能够和字符串P开头的3个字符匹配,这里的P[4-6]就组成了一个盒子,所以该算法被形象的称为Z-BOX算法。
二 Z-BOX算法的计算过程
在计算Zi(P)值的时候,我们可以采用递推的方法。假设现在我们已经知道了Z0(P)至Zi(P)的值,我们如何求Zi+1(P)的值?
首先,我们需要进一步明确BOX的概念,还是用上面的模式串P = aabaaabd来举例,i=5这个位置,也就是P[5],其实同时被2个BOX覆盖,因为在Z4(P)和Z5(P)中都包含了P[5]。所以我们再定义两个值:left和right,表示对于i位置,包含了P[i]的所有BOX中右边值最大的BOX的范围。
所以当i=5时,left5 = 4,right5 = 6。
接下来我们分析如何得到Zi+1(P)的值。假设Zi(P)时,left,right的值如下图所示(图中k位置表示i+1)。
情况1:
k在right左边,left,right所确定的范围(红色标记为a的box)是一个box的话,那么a有一个从模式串开头匹配的范围a’。
所以在a范围内的k,必然在a’中有一个对应的k’,Zk’(P)的值=b,也就是图中绿色框的范围b,如果b的范围在a的范围之内,则Zk(P) = b = Zk’(P)。
情况2:
k在right左边或k=right,但是k对应的k’处的Zk’(P)的值超过了(或等于)a’的范围。此时,我们可以确定的是k到right之间的字符和0到right-k之间的字符是匹配的,right之后的字符是否匹配,则需要我们逐个字符去验证。当我们找到最长的匹配串之后,我们就可以得到Zk(P)的值,同时需要更新left和right的数值为:left = k,right = 匹配的最右端下标。
情况3:
如果k > right,此时a box将不能给我们提供有用的辅助了,我们只能从k位置逐个字符去检验是否和模式串的前缀匹配。如果有能够匹配的前缀,那么我们更新Zk(P)的值,同时也更新left和right的数值。
上面3种情况说的比较抽象,下面我们来看一个具体的例子。
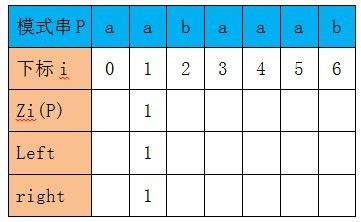
对于模式串P = aabaaab,我们从0下标开始计数,并初始化left = right = 0,我们从下标为1的字符开始计算Zi(P)的值。
因为P[1] = P[0],且P[2] != P[1],所以Z1(P) = 1,left = 1,right = 1。
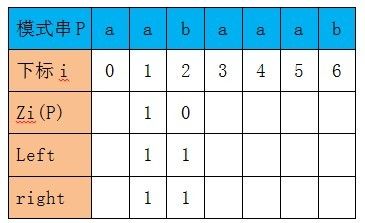
接下来计算Z2(P),2 > right(值为1),所以此时满足情况3,从P[2]开始进行匹配检查,P[2] != P[0]。所以left,right的值不变,Z2(P) = 0。
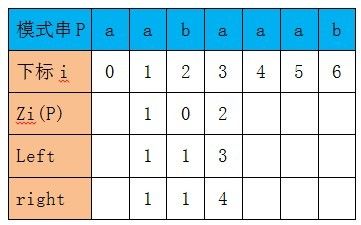
再来看Z3(P),依然是情况3(i > right),不同的是此时有能够匹配上的字符P[3,4] = P[0,1],所以Z3(P) = 2,同时更新left = 3,right = 4。
再来看Z4(P),此时i <= right,所以不满足 情况3了,这时把box(P[3,4])搬到模式串开头的话(P[3]对应到P[0]位置),i对应的就是1,所以i’ = 1。
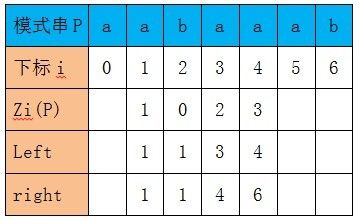
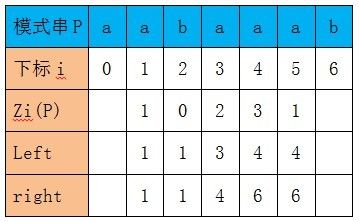
Zi’(P) = Z1(P) = 1。所以Z4(P)对应的box大小至少为1,而此时right = 4,下标4 + (下标1处的box大小-1)= 4(>= right)(也就是从当前下标处加上Zi’(p)的值到达或者超过了right的值),所以满足情况2,能够匹配的部分我们就不用再匹配了(P[4] = P[0]),我们直接从匹配部分的后面开始进行比较,也就是从P[5]和P[1]开始继续比较,P[5]=P[1],P[6]=P[2]。得到的结果如下:
情况2比较少遇到,且多绕一个弯,需要读者好好揣摩。我在一开始没有见到这个例子的时候,也是没想通,怎么会存在这种情况呢?当时我认为只有情况1,不会有情况2,后来看到这个例子才明白过来,自己大脑里面少转了一个弯。
求Z5(P)时,i’ = 5 - left = 5 - 4 = 1,Z1(P) = 1,下标5 + (下标1处的box大小-1)= 5(< right),满足情况1,所以Z5(P) = Z1(P) = 1。left和right值不变。
同样Z6(P)也满足情况1。
三 Z-BOX算法的代码实现(C语言版)
经过上面例子的具体分析我们可以写出Z-BOX算法的代码
#include <string.h>
#include <stdio.h>
void ZBox(const char* pattern, unsigned int length, unsigned int zbox[])
{
zbox[0] = 0;
unsigned int left = 0;
unsigned int right = 0;
for (unsigned int i = 1; i < length; i++)
{
if (i > right)//情况3
{
int n = 0;
for ( ; pattern[n] == pattern[i+n]; n++);
if (0 != n)
{
right = i+n-1;
left = i;
}
zbox[i] = n;
}
else
{
if (zbox[i-left] < right-i+1)//情况1
{
zbox[i] = zbox[i-left];
}
else//情况2
{
int n = 1;
for (;pattern[right-i+n] == pattern[right+n]; n++);
zbox[i] = right-i+n;
right += n-1;
left = i;
}
}
printf(" zbox[%d] = %d, left is %d, right is %d\r\n", i, zbox[i], left, right);
}
}
int main(int argc, char* argv[])
{
const char pattern[] = "aabaaab";
unsigned int zbox[100];
ZBox(pattern, strlen(pattern), zbox);
return 0;
}
上面的程序输出结果为:
zbox[1] = 1, left is 1, right is 1
zbox[2] = 0, left is 1, right is 1
zbox[3] = 2, left is 3, right is 4
zbox[4] = 3, left is 4, right is 6
zbox[5] = 1, left is 4, right is 6
zbox[6] = 0, left is 4, right is 6
zbox[2] = 0, left is 1, right is 1
zbox[3] = 2, left is 3, right is 4
zbox[4] = 3, left is 4, right is 6
zbox[5] = 1, left is 4, right is 6
zbox[6] = 0, left is 4, right is 6
和我们在前面递归推导的结果一致。
四 Z-BOX算法在具体的模式匹配、字符串查找中的应用
要想使用Z-BOX算法进行字符串查找,我们将要查找的模式串放在被查找目标串的开头部分组成一个新的串P,然后从前向后依次计算每一个位置的Zi(P)值(i从0开始计数)。当i >= length(模式串),且Zi(P) >= length(模式串),则i位置是一个查找到的匹配位置。
以下是实现代码:
#include <string.h>
#include <stdio.h>
int SearchWithZBox(const char* dest, const char* pattern)
{
int nDlen = strlen(dest);
int nPlen = strlen(pattern);
char *str = new char[nDlen+nPlen];
if (!str)
{
goto Exit0;
}
int *Z = new int[nDlen+nPlen];
if (!Z)
{
goto Exit0;
}
memcpy(str, pattern, nPlen);
memcpy(str+nPlen, dest, nDlen);
//create z box
Z[0] = 0;
int l = 0;
int r = 0;
for (int i = 1; i < nDlen+nPlen; i++)
{
if (i > r)
{
int n = 0;
for (; str[i+n] == str[n]; n++);
if (n > 0)
{
l = i;
r = i+n-1;
}
Z[i] = n;
}
else
{
if (Z[i-l] < r-i+1)
{
Z[i] = Z[i-l];
}
else
{
int n = 1;
for (int s = r-i; str[s+n] == str[r+n]; n++);
Z[i] = r-i+n;
l = i;
r = r+n-1;
}
}
if (i >= nPlen && Z[i] >= nPlen)
{
printf("Search With ZBox Find at %d\r\n", i - nPlen);
}
}
Exit0:
if (str)
{
delete str;
str = NULL;
}
if (Z)
{
delete Z;
Z = NULL;
}
return -1;
}
int main(int argc, char* argv[])
{
// 0 1 2 3 4 5
// 012345678901234567890123456789012345678901234567890123456789
const char dest[] = "demoxdemoaaabaaaxdembbaaaddemobaaababdemoooabcxbaabaaadddemo";
const char pattern[] = "aabaaab";
unsigned int zbox[100];
//ZBox(pattern, strlen(pattern), zbox);
SearchWithZBox(dest, "demo");
return 0;
}
Search With ZBox Find at 0
Search With ZBox Find at 5
Search With ZBox Find at 26
Search With ZBox Find at 37
Search With ZBox Find at 56
Search With ZBox Find at 5
Search With ZBox Find at 26
Search With ZBox Find at 37
Search With ZBox Find at 56
表示在目标串dest中的下标为0,5,26,37,56位置处找到了模式串“demo”。经验证正确且无遗漏。
五 总结
Z-BOX算法思路并不复杂,代码也不难写出,唯一有点绕的地方是对情况2的理解和处理。其算法时间复杂度是线性的,但实际应用中比较少见该算法,大概是因为要使用Z-BOX算法需要将模式串和目标串先组合起来,这需要额外的空间,另外用于辅助的Z-BOX数组也要求该算法的空间复杂度达到了O(len(P)+len(D))(模式串长度和目标串长度之和)。基于这些原因导致Z-BOX算法在实际应用中成为鸡肋。不过了解该算法的思路对于开阔我们的思维不无裨益,而且该算法可以应用到KMP、BM算法的求模式串最长匹配子串中,可以加速模式串的处理过程,我们在以后的文章中会提到。
六 参考资料
http://binfalse.de/2010/09/advanced-searching-via-z-algorithm/
这篇英文文章提供的例子很好的覆盖了3种情况
http://blog.csdn.net/joylnwang/article/details/6878068
这篇博客中的图片很形象的说明了情况1和情况2
Algorithms.on.Strings.Trees.and.Sequences].(Dan.Gusfield).pdf
这是一本全面介绍字符串处理算法的书籍,我没有找到中文版,这是英文版
===============本文完===============