KMeans聚类算法思想与可视化

1.聚类分析

1.0 概念

聚类分析简称聚类（clustering），是一个把数据集划分成子集的过程，每一个子集是一个簇（cluster），使得簇中的样本彼此相似，但与其他簇中的样本不相似。

聚类分析不需要事先知道样本的类别，甚至不用知道类别个数，因此它是一种无监督的学习算法，一般用于数据探索，比如群组发现和离群点检测，还可以作为其他算法的预处理步骤。

下面的动图展示的是一个聚类过程，感受一下：

1.1 基本聚类方法

主要的聚类算法一般可以划分为以下几类：

方法	一般特点
划分方法	1.发现球形互斥的簇 2.基于距离 3.可用均值或中心点代表簇中心 4.对中小规模数据有效
层次方法	1.聚类是一个层次分解 2.不能纠正错误的合并或划分 3.可以集成其他技术
基于密度的方法	1.可以发现任意形状的簇 2.簇是对象空间中被低密度区域分隔的稠密区域 3.簇密度 4.可能过滤离群点
基于网格的方法	1.使用一种多分辨率网格数据结构 2.快速处理

.
上面的内容节选自韩家炜的《数据挖掘》，该书中的第十和第十一章对聚类算法进行了详细的介绍。等我详细学习后再对聚类分析做个总结，这篇文章则把重点放在简单的Kmeans算法上，Kmeans算法属于上面分类中的划分方法。

2.Kmeans算法思想

2.0 算法步骤

Kmeans算法(k均值算法)是一种简单的聚类算法，属于划分式聚类算法，当给定一个数据集D时，Kmeans算法的步骤如下：

选择K个点作为初始质心（随机产生或者从D中选取）  
repeat  
    将每个点分配到最近的质心，形成K个簇  
    重新计算每个簇的质心  
until 簇不发生变化或达到最大迭代次数  

若n是样本数，m是特征维数，k是簇数，t是迭代次数，则Kmeans算法的时间复杂度为O(tknm)，与样本数量线性相关，所以在处理大数据集合时比较高效，伸缩性好。空间复杂度为O((n+k)*m)。

Kmens算法虽然一目了然，但算法实现过程中涉及到的细节也不少，下面逐一介绍。

2.0 k值选取

k的值是用户指定的，表示需要得到的簇的数目。在运用Kmeans算法时，我们一般不知道数据的分布情况，不可能知道数据的集群数目，所以一般通过枚举来确定k的值。另外，在实际应用中，由于Kmean一般作为数据预处理，或者用于辅助分类贴标签，所以k一般不会设置很大。

2.1 初始质心的选取

Kmeans算法对初始质心的选取比较敏感，选取不同的质心，往往会得到不同的结果。初始质心的选取方法，常用以下两种的简单方法：一种是随机选取，一种是用户指定。
需要注意的是，无论是随机选取还是用户指定，质心都尽量不要超过原始数据的边界，即质心每一维度上的值要落在原始数据集每一维度的最小与最大值之间。

2.2 距离度量方法

距离度量方法（或者说相似性度量方法）有很多种，常用的有欧氏距离，余弦相似度，街区距离，汉明距离等等。在Kmeans算法中，一般采用欧氏距离计算两个点的距离，欧氏距离如下：

distEclud(X,Y)=∑i=1n(Xi−Yi)2−−−−−−−−−−−√

举个例子，X=（1000，0.1），Y=（900，0.2）,那么它们的欧氏距离就是：

(1000−900)2+(0.1−0.2)2−−−−−−−−−−−−−−−−−−−−−−√≈100

举这个例子是为了说明，当原始数据中各个维度的数量级不同时，它们对结果的影响也随之不同，那些数量级太小的维度，对于结果几乎没产生任何影响。比如所举的例子中的第二个维度的0.1，0.2，与第一个维度1000的数量级相差了一万倍。

为了赋予数据每个维度同等的重要性，我们在运用欧氏距离时，必须先对数据进行规范化，比如将每个维度都缩放到[0,1]之间。

2.3 质心的计算

在Kmeans算法中，将簇中所有样本的均值作为该簇的质心。这也是Kmeans名字的由来吧。

2.4 算法停止条件

在两种情况下算法应该停止：一种是达到了指定的最大迭代次数，一种是算法已经收敛，即各个簇的质心不再发生变化。关于算法的收敛，在2.5部分讨论。

2.5 代价函数与算法收敛

Kmeans算法的代价函数比较简单，就是每个样本点与其所属质心的距离的平方和（误差平方和，Sum of Squared Error,简称SSE）：

J(c,u)=∑i=1k||X(i)−uc(i)||2

与其他机器学习算法一样，我们要最小化这个代价函数，但这个函数没有解析解，所以只能通过迭代求解的方法来逼近最优解（这一点也和众多机器学习算法一样吧）。所以你再看看算法步骤，其实就是一个迭代过程。

由于代价函数（SSE）是非凸函数，所以在运用Kmeans算法时，不能保证收敛到一个全局的最优解，我们得到的一般是一个局部的最优解。

因此，为了取得比较好的效果，我们一般会多跑几次算法（用不同的初始质心），得到多个局部最优解，比较它们的SSE，选取SSE最小的那个。

3.Kmeans算法实现

3.1 代码

这是采用Python编写，基于数值计算库Numpy实现的Kmeans算法，参考了Scikit Learn的设计，将Kmeans封装成一个class，对于代码简要说明如下，具体的可以在这里查看：代码链接。

class KMeans(object):

    def __init__(self,n_clusters=5,initCent='random',max_iter=300):
        #n_clusters表示聚类个数，相当于k
        #initCent表示质心的初始化方式，可以设为'random'或指定一个数组
        #max_iter表示最大的迭代次数

    def _distEclud(self, vecA, vecB):
        #计算两点的欧式距离

    def _randCent(self, X, k):
        #随机选取k个质心,必须在数据集的边界内

    def fit(self, X):
        #调用fit方法，对数据集X聚类
        #聚类完后将得到质心self.centroids,簇分配结果self.clusterAssment 

    def predict(self,X):
        #根据聚类结果，预测新输入数据所属的族
        #其实就是计算每个点与各个质心self.centroids的距离

3.2 实例

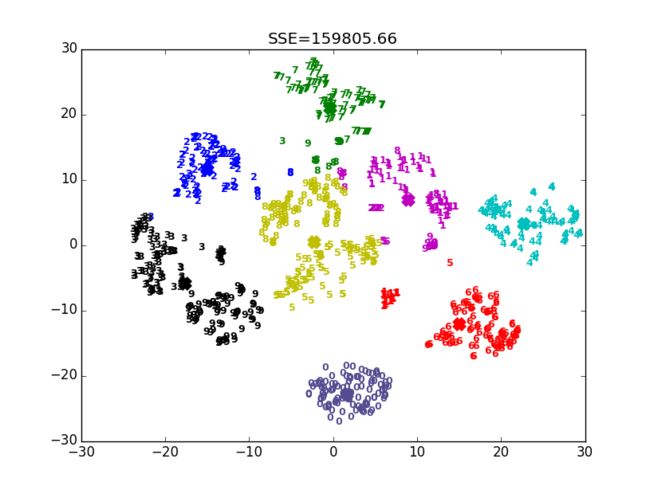
下面看一个简单的例子，首先是数据集的准备，文章开头展示的图片来自于这份数据data.pkl，是经典的手写数字MNIST数据库，我从中选取1000张（包括0～9共十种数字），用t_sne降到了2维（为了可视化）。

首先，加载数据集：

import cPickle
X,y = cPickle.load(open('data.pkl','r'))  #X和y都是numpy.ndarray类型
X.shape  #输出(1000,2)
y.shape  #输出(1000,)对应每个样本的真实标签

对该数据集进行聚类分析，聚类个数设置为10(因为有十种数字)，质心初始化方式为随机初始化，最大迭代次数设置为100。并利用matplotlib画出聚类结果：

import numpy as np
import matplotlib.pyplot as plt
from kmeans import KMeans
clf = KMeans(n_clusters=10,initCent='random',max_iter=100)
clf.fit(X)
cents = clf.centroids#质心
labels = clf.labels#样本点被分配到的簇的索引
sse = clf.sse
#画出聚类结果，每一类用一种颜色
colors = ['b','g','r','k','c','m','y','#e24fff','#524C90','#845868']
n_clusters = 10
for i in range(n_clusters):
    index = np.nonzero(labels==i)[0]
    x0 = X[index,0]
    x1 = X[index,1]
    y_i = y[index]
    for j in range(len(x0)):
        plt.text(x0[j],x1[j],str(int(y_i[j])),color=colors[i],\
                fontdict={'weight': 'bold', 'size': 9})
    plt.scatter(cents[i,0],cents[i,1],marker='x',color=colors[i],linewidths=12)
plt.title("SSE={:.2f}".format(sse))
plt.axis([-30,30,-30,30])
plt.show()

得到的结果如下,可见效果并不好，5和8，3和9都被混为一类：

而且，不改动上面的代码，每一次得到的结果也不一样，这是因为Kmeans聚类对于初始质心的选取是敏感的，而上面的代码中我们采用随机初始化质心的方式。当然，我们也可以采取指定初始质心的方式，只需要改一行代码：

clf = KMeans(n_clusters=10,initCent=X[0:10],max_iter=100) 

文章开头的动图，是固定质心为X[50:60]，迭代1～5次得到的，限于文章篇幅，代码不贴上来，放在test.py

4.二分Kmeans算法

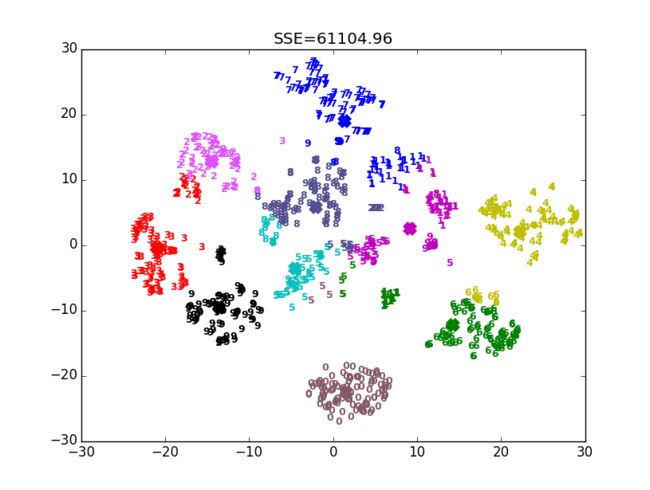
二分Kmeans算法（bisecting Kmeans）是为了克服Kmeans算法收敛于局部最小值的问题而提出的。该算法首先将所有点作为一个簇，然后将该簇一分为二。之后选择其中一个簇继续划分，选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值，上述过程不断迭代，直到得到用户指定的簇数目为止。算法步骤如下：

将所有数据点看成一个簇 当簇数目小于k时 对每一个簇 计算总误差(sse_origin) 在给定的簇上面进行k-均值聚类（k=2） 计算将该簇一分为二后的总误差(sse_new) 选择使得误差(sse_new)最小的那个簇进行划分操作

根据这个步骤，不难写出二分Kmeans算法的代码，同样地，我将其封装成class，源码放在这里，其使用方法如下：

import numpy as np
import matplotlib.pyplot as plt
from kmeans import biKMeans
n_clusters = 10
clf = biKMeans(n_clusters)
clf.fit(X)
cents = clf.centroids
labels = clf.labels
sse = clf.sse
#画出聚类结果，每一类用一种颜色
colors = ['b','g','r','k','c','m','y','#e24fff','#524C90','#845868']
for i in range(n_clusters):
    index = np.nonzero(labels==i)[0]
    x0 = X[index,0]
    x1 = X[index,1]
    y_i = y[index]
    for j in range(len(x0)):
        plt.text(x0[j],x1[j],str(int(y_i[j])),color=colors[i],\
                fontdict={'weight': 'bold', 'size': 9})
    plt.scatter(cents[i,0],cents[i,1],marker='x',color=colors[i],linewidths=12)
plt.title("SSE={:.2f}".format(sse))
plt.axis([-30,30,-30,30])
plt.show()

得到下图，可以发现效果也并不是特别好，并且多次运行上面的代码，结果也是不一样的，这是因为二分Kmeans算法在“二分”的时候，采取的也是随机初始化质心的方式。

5.参考

• 《数据挖掘》韩家炜
• 《机器学习实战》
• 《基本kmeans算法介绍及其实现》

转载请注明出处：http://blog.csdn.net/u012162613/article/details/47811235