【巧妙算法系列】【Uva 11464】 - Even Parity 偶数矩阵

偶数矩阵（Even Parity, UVa 11464）

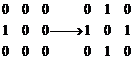
给你一个n×n的01矩阵（每个元素非0即1），你的任务是把尽量少的0变成1，使得每个元素的上、下、左、右的元素（如果存在的话）之和均为偶数。比如，如图1-6（a）所示的矩阵至少要把3个0变成1，最终如图1-6（b）所示，才能保证其为偶数矩阵。

  （a）                 (b)

【输入格式】

输入的第一行为数据组数T（T≤30）。每组数据的第一行为正整数n（1≤n≤15）；接下来的n行每行包含n个非0即1的整数，相邻整数间用一个空格隔开。

【输出格式】

对于每组数据，输出被改变的元素的最小个数。如果无解，应输出-1。

思路：

   这道题是一道经典的枚举+模拟综合运用的算法 

   枚举第一排0 1的变化 以此模拟出第二排至第N排的变化

  复杂度为    o（(2^n)*n*n）

书上的分析：

也许最容易想到的方法就是枚举每个数字“变”还是“不变”，最后判断整个矩阵是否满足条件。遗憾的是，这样做最多需要枚举2²⁵⁵≈5×10⁶⁷种情况，实在难以承受。

注意到n只有15，第一行只有不超过2¹⁵=32 768种可能，所以第一行的情况是可以枚举的。接下来根据第一行可以完全计算出第二行，根据第二行又能计算出第三行（想一想，如何计算），以此类推，这样，总时间复杂度即可降为O(2ⁿ×n²)。

我的代码如下：

#include<cstdio>
#include<cstring>
using namespace std;
int map[20][20];
int tempmap[20][20];
int ans,n;
int getans(int KT)
{
	memset(tempmap,0,sizeof(tempmap));
	int cnt=0,temp,k;
	for(int i=1;i<=n;i++)
	{
		temp=KT&1;
		KT=KT>>1;
		tempmap[1][i]=temp;
		if(tempmap[1][i]!=map[1][i]) 
		  if(temp==1) cnt++;
		  else return 0;
	}
	for(int i=2;i<=n;i++)
	 for(int j=1;j<=n;j++)
	  {
	  k=tempmap[i-1][j-1]+tempmap[i-1][j+1]+tempmap[i-2][j];
	  if(k%2==1) tempmap[i][j]=1;
	  else tempmap[i][j]=0;
	  
	  if(tempmap[i][j]!=map[i][j])  
		  if(tempmap[i][j]==1) cnt++;
		  else return 0;
	  }
	if(cnt<ans) ans=cnt;
	return 0;
}
int main()
{
	//freopen("a.in","r",stdin);
	//freopen("a.out","w",stdout);
	int T;
	scanf("%d",&T);
	int maxn;
	int TT=T;
	while(T--)
	{
		ans=2000000000;
		scanf("%d",&n);
		maxn=(1<<n)-1;
		for(int i=1;i<=n;i++)
		   for(int j=1;j<=n;j++)
		   	 scanf("%d",&map[i][j]);
		for(int i=0;i<=maxn;i++)
		getans(i);
		if(ans==2000000000) ans=-1;
	    printf("Case %d: %d\n",TT-T,ans);
	}
	return 0;
}