曲线拟和函数lsqcurvefit & nlinfit

转载自：http://panda0411.com/2011/08/29/curve-fit-and-function-lsqcurvefitnlinfit/

琢磨了好久matlab自带的曲线拟和工具箱, 发现这货只能解决从离散数据得到各种类型的拟和效果, 但是反之貌似没法实现, google一下有这两个函数可以用:
lsqcurvefit和nlinfit

lsqcurvefit(非线性最小二乘法)
help了一下, 发现官方的文档过于详尽, 节选部分吧.
LSQCURVEFIT solves non-linear least squares problems.

X = LSQCURVEFIT(FUN,X0,XDATA,YDATA) starts at X0 and finds coefficients X to best fit the nonlinear functions in FUN to the data YDATA (in the least-squares sense).

FUN accepts inputs X and XDATA and returns a vector (or matrix) of function values F, where F is the same size as YDATA, evaluated at X and XDATA.

NOTE: FUN should return FUN(X,XDATA) and not the sum-of-squares sum((FUN(X,XDATA)-YDATA).^2).

((FUN(X,XDATA)-YDATA) is squared and summed implicitly in the algorithm.)

这里面对函数的各个参数的意义和用法都做了解释.
[x,resnorm]=lsqcurvefit(fun,x0,xdata,ydata,...)
fun 是我们需要拟合的函数，这是重点
x0 是我们对函数中各参数的预测值，这也是重点
xdata 则是横轴坐标的值
ydata 是纵轴的值
需要注意的是lsqcurvefit里面的fun是我们需要拟和的函数, 需要另外编写.

下面用以前某年的CUMCM真题修改作为示例.

--------------------------------------------------------------------------------------------
tj/s                      | 100  | 200  | 300  | 400  | 500  | 600  | 700  | 800  | 900  | 1000 |
--------------------------------------------------------------------------------------------
Cj/(mg*cm-3) | 4.54  | 4.99 | 5.35  | 5.65  | 5.90 | 6.10  | 6.26  | 6.39 | 6.50  |  6.59 |
--------------------------------------------------------------------------------------------
在已知部分参数的情况下, 求函数

E(K,aA,aB)=∑j=110[a+be−0.02Ktj−Cj]

求函数的最下值的点(K,a,b)

1. 编写M文件(curvefun.m)

function f = curvefun(x,tdata)
f = x(1)+x(2)*exp(-0.02*x(3)*tdata);
end

2. 编写程序(test1.m)

tdata = linspace(100,1000,10);
cdata = 1e-05.*[454 499 535 565 590 610 626 639 650 659];
x0 = [0.2 0.05 0.05];
x = lsqcurvefit(@curvefun, x0, tdata, cdata);
f = curvefun(x, tdata)
plot(tdata, cdata, '*', tdata, f, 'r-')

3. 输出结果
x= 0.0069 -0.0029 0.0809
即表示k=0.2542, a=0.0063, b=-0.0034

nlinfit

从matlab给出的帮助文档来看, nlinfit与lsqcurvefit同属与非线性最小二乘拟和, 一般来说都是能得到比较接近的结果.
但是由于nlinfit使用的是牛顿方法, 在使用是需要给出你和参数的假设初值, 有些问题对初值比较敏感, 不同的初值会导致差异比较大.
下面示例nlinfit的用法:

混凝土的抗压强度随着养护时间的延长而增加, 现将一批混凝土作成12个试块, 记录了养护日期x(日)以及抗压强度y(kg/cm2)的数据

-------------------------------------------------------------------------------------------------------
养护时间x |    2     |    3     |     4   |     5   |     7    |     9    |   12    |    14   |    17   |    21   |   28   |  56    |
-------------------------------------------------------------------------------------------------------
抗压强度y | 35+r | 42+r | 47+r | 53+r | 59+r | 65+r | 68+r | 73+r | 76+r | 82+r | 86+r | 99+r |
--------------------------------------------------------------------------------------------------------
建立非线性回归模型, 对得到的模型和系数进行检验.
注明：此题中的+r代表加上一个[-0.5,0.5]之间的随机数

y=a+k1emx+k2e−mx

1. 编写m文件(myfunc.m)

function f = myfunc(beta, x)
f = beta(1)+beta(2)*exp(beta(4)*x)+beta(3)*exp(-beta(4)*x);
end

2. 编写程序

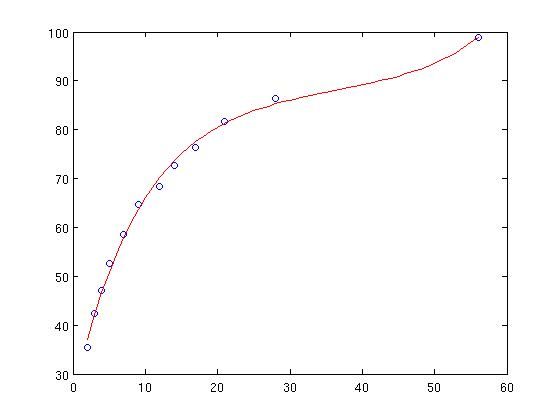
clc;clear;
x=[2 3 4 5 7 9 12 14 17 21 28 56];
r=rand(1,12)-0.5; %rand产生的是0,1之间的随机数, 这里表示产生12个[-0.5 0.5]之间的随机数
y1=[35 42 47 53 59 65 68 73 76 82 86 99];
y=y1+r
beta=nlinfit(x,y,@myfunc,[0.5 0.5 0.5 0.5]); %nlinfit的语法与lsqcurvefit基本类似, 只是参数的顺序上有些差异, 这里不再赘述
a=beta(1),k1=beta(2),k2=beta(3),m=beta(4)
%test the model
xx=min(x):max(x);
yy=a+k1*exp(m*xx)+k2*exp(-m*xx);
plot(x,y,'o',xx,yy,'r')

当然, 这里如果不想另外编写m函数, 可以使用上一篇笔记中的内联函数inline来实现. 只需要将程序里面的beta=.....替换成下面两行即可, 注意替换后的nlinfit不需要使用@符号了.

myfunc=inline('beta(1)+beta(2)*exp(beta(4)*x)+beta(3)*exp(-beta(4)*x)','beta','x');
beta=nlinfit(x,y,myfunc,[0.5 0.5 0.5 0.5]);

3. 输出结果

a = 88.0591, k1 = 0.0318, k2 = -62.7924, m = 0.1044