hdu 4421 Bit Magic(two-SAT+思维)
Bit Magic
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 1628 Accepted Submission(s): 469
Problem Description
Yesterday, my teacher taught me about bit operators: and (&), or (|), xor (^). I generated a number table a[N], and wrote a program to calculate the matrix table b[N][N] using three kinds of bit operator. I thought my achievement would get teacher's attention.
The key function is the code showed below.
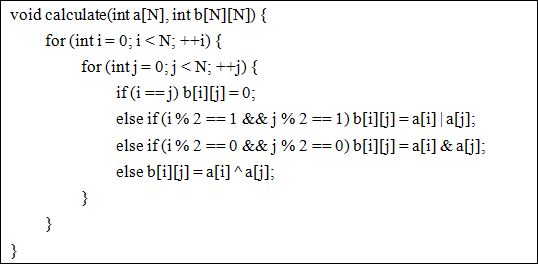
There is no doubt that my teacher raised lots of interests in my work and was surprised to my talented programming skills. After deeply thinking, he came up with another problem: if we have the matrix table b[N][N] at first, can you check whether corresponding number table a[N] exists?
The key function is the code showed below.
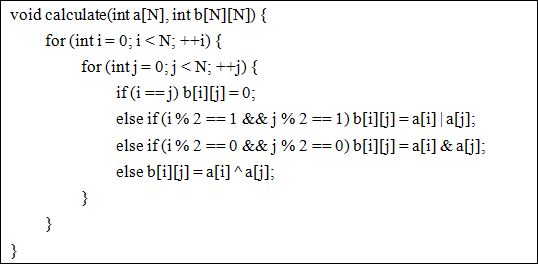
There is no doubt that my teacher raised lots of interests in my work and was surprised to my talented programming skills. After deeply thinking, he came up with another problem: if we have the matrix table b[N][N] at first, can you check whether corresponding number table a[N] exists?
Input
There are multiple test cases.
For each test case, the first line contains an integer N, indicating the size of the matrix. (1 <= N <= 500).
The next N lines, each line contains N integers, the jth integer in ith line indicating the element b[i][j] of matrix. (0 <= b[i][j] <= 2 31 - 1)
For each test case, the first line contains an integer N, indicating the size of the matrix. (1 <= N <= 500).
The next N lines, each line contains N integers, the jth integer in ith line indicating the element b[i][j] of matrix. (0 <= b[i][j] <= 2 31 - 1)
Output
For each test case, output "YES" if corresponding number table a[N] exists; otherwise output "NO".
Sample Input
2 0 4 4 0 3 0 1 24 1 0 86 24 86 0
Sample Output
YES NO
Source
2012 Asia ChangChun Regional Contest
Recommend
zhuyuanchen520 | We have carefully selected several similar problems for you: 4822 4821 4820 4819 4818
题意:
首先用长度为n的A[]数组构造出B[i][j]数组。当i==j时B[i][j]=0.当i,j同时为奇数时.B[i][j]=A[i]|A[j]。当i,j同时为偶数时
B[i][j]=A[i]&a[j]。当i,j一奇一偶时。B[i][j]=A[i]^A[j]。现给你B数组。问有没有符合条件的A数组。 (0 <= B[i][j] <= 2 31 - 1)
思路:
在two-SAT题集里找到的这道题。开始一直没想到和two-SAT有什么关系。因为two-SAT针对的每个节点只有两种选择而这题B[i]的范围却那么大。那么多选择这么搞都不行。后来想想既然是位操作那么直接把A看做二进制。根据B的范围A[i]最多就31个二进制位。如果A[i]的每个二进制位在B的约束条件下都有解。那么A一定有解啦。所以我们可以对1-第31位二进制位根据B数组建立约束条件。然后two-SAT判断可行性。如果所有位都有解自然YES如果有一位无解就NO。
详细见代码:
#include<algorithm>
#include<iostream>
#include<string.h>
#include<sstream>
#include<stdio.h>
#include<math.h>
#include<vector>
#include<string>
#include<queue>
#include<set>
#include<map>
//#pragma comment(linker,"/STACK:1024000000,1024000000")
using namespace std;
const int INF=0x3f3f3f3f;
const double eps=1e-8;
const double PI=acos(-1.0);
const int maxn=510;
//typedef __int64 ll;
struct TSAT
{
int n,ct,s[maxn];
bool vis[maxn<<1];
vector<int> eg[maxn<<1];
void init(int N)
{
n=N;
for(int i=2*n-1;i>=0;i--)
eg[i].clear();
memset(vis,0,sizeof vis);
}
void adde(int x,int xv,int y,int yv)//建边x的xv状态会与y的yv状态冲突
{
x=x*2+xv;
y=y*2+yv;
eg[x].push_back(y^1);
eg[y].push_back(x^1);
}
bool dfs(int x)//顺着必选边走看是否冲突
{
if(vis[x^1])
return false;
if(vis[x])
return true;
vis[x]=true;
s[ct++]=x;
for(int i=0;i<eg[x].size();i++)
if(!dfs(eg[x][i]))
return false;
return true;
}
bool solve()
{
for(int i=0;i<2*n;i+=2)
{
if(!vis[i]&&!vis[i+1])
{
ct=0;
if(!dfs(i))
{
while(ct)
vis[s[--ct]]=false;
if(!dfs(i+1))
return false;
}
}
}
return true;
}
} tool;
int B[maxn][maxn];
int main()
{
int i,j,n,u,v,base,p;
bool op,flag;
while(~scanf("%d",&n))
{
for(i=0;i<n;i++)
for(j=0;j<n;j++)
scanf("%d",&B[i][j]);
for(p=0,base=1;p<32;p++)//分别看二进制第p位是否冲突。若每一位都不冲突。肯定就有合法解
{
tool.init(n);
for(i=0;i<n;i++)
{
for(j=i+1;j<n;j++)
{
op=B[i][j]&base;//取出第p位
if((i&1)&&(j&1))
{
for(u=0;u<2;u++)
for(v=0;v<2;v++)
if((u|v)!=op)
tool.adde(i,u,j,v);
}
else if(!(i&1)&&!(j&1))
{
for(u=0;u<2;u++)
for(v=0;v<2;v++)
if((u&v)!=op)
tool.adde(i,u,j,v);
}
else
{
for(u=0;u<2;u++)
for(v=0;v<2;v++)
if((u^v)!=op)
tool.adde(i,u,j,v);
}
}
}
flag=tool.solve();
if(!flag)
break;
base<<=1;
}
if(flag)
printf("YES\n");
else
printf("NO\n");
}
return 0;
}
时限2000MS过的好惊险。不知道是算法的问题还是用了STL的缘故。看大牛只用了140MS表示膜拜。。。。。