[置顶] 【机器学习笔记3】Stanford公开课Exercise 2——Linear Regression
Stanford公开课Exercise 2原题地址:http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=MachineLearning&doc=exercises/ex2/ex2.html。看Stanford的机器学习公开课真是舒服,视频讲解的非常清楚,练习也布置的非常好,把所有重要内容总结了一遍,给出了很多参考信息,让读者非常清晰的知道怎么去做。下面是我完成的笔记。
(一)原理回顾
简单重复一下实现的过程,具体的看上一篇(【机器学习笔记】Linear Regression总结):
1. h(θ)函数
2. J(θ)函数
向量化后简化为:
3. θ迭代过程
向量化后简化为:
(二)实现代码
原题中给出了详细的步骤和提示,下面的代码是根据原题中的提示实现的,代码中加有注释,这里不再对代码进行解释。
%============================================= % Exercise 2: Linear Regression % author : liubing ([email protected]) % %LB_c: 加载数据 =============== x = load("ex2x.dat"); y = load("ex2y.dat"); %LB_c: 矩阵x第一列加上全1 x = [ones(size(x)(1),1), x]; %============================== %LB_c: 常量数据准备=========================================== iter_total = 1500; %theta更新的迭代次数 %m为样本数,n为特征数(包含第一列的常数项,实际特征数为n-1) [m,n] = size(x); alpha = 0.07; %============================================================= %LB_c: 迭代过程 ================================================================ theta = zeros(n,1); %theta初始化为全0,其他值也可以 J = zeros(iter_total,1); %存储每一步迭代的J(theta)值 for iter_index = [1:iter_total] J(iter_index) = (x*theta-y)' * (x*theta-y) / (2*m); %求当前的J(theta),参考上面的(公式3) err = x * theta - y; grad = ( x' * err ) / m; %求gradient theta = theta - alpha * grad; %梯度下降法更新theta,参考上面的(公式5) end %=============================================================================== %LB_c: 结果绘制 ============================================= %绘制J(theta)迭代过程 figure; plot([1:iter_total], J'); xlabel('iteration (times)'); ylabel('J(theta)'); axis([1,1550, 0, 0.6]); %绘制训练数据 figure; plot(x(:,2), y, 'o', 'Markersize', 3); xlabel('Age (years)'); ylabel('Height (meters)'); %绘制回归结果 hold on; plot(x(:,2), x*theta, 'r-'); legend('Training data', 'Regression result'); %绘制J(theta)曲面 theta0_vals = linspace(-3,3,100); theta1_vals = linspace(-1,1,100); J_arr = zeros(length(theta0_vals), length(theta1_vals)); for i = [1:length(theta0_vals)] for j = [1:length(theta1_vals)] t = [theta0_vals(i); theta1_vals(j)]; J_arr(i,j) = (x*t-y)' * (x*t-y) / (2*m); %求J(theta),参考上面的(公式3) end end J_arr = J_arr'; figure; surf(theta0_vals, theta1_vals, J_arr); xlabel('theta0'); ylabel('theta1'); zlabel('J(theta)'); %绘制J(theta)等高线图 figure; contour(theta0_vals, theta1_vals, J_arr, logspace(-2,2,15)); xlabel('theta0'); ylabel('theta1'); %============================================================ %LB_c: theta结果输出与测试 ================= printf('result of theta : '); theta printf('result of testing data(age=3.5):'); [1,3.5]*theta printf('result of testing data(age=7):'); [1,7]*theta %===========================================
(三)执行结果
1. 训练样本及回归结果(直线)
2. J(θ)函数迭代变化趋势
3. J(θ)函数相对于theta0和theta1的变化趋势(曲面图)
4. J(θ)函数相对于theta0和theta1的变化趋势(等高线图)
5. 最终的回归系数(theta)结果及使用该回归系数对测试数据(age=3.5和age=7)进行预测的结果
最终显示的结果与原题中给出的结果基本一致。

![[置顶] 【机器学习笔记3】Stanford公开课Exercise 2——Linear Regression_第1张图片](http://img.e-com-net.com/image/info5/68f990f16525478482ba2253a1170827.jpg)
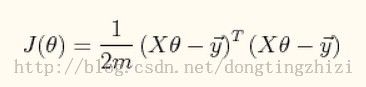
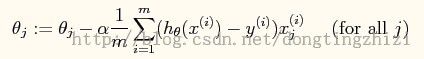
![[置顶] 【机器学习笔记3】Stanford公开课Exercise 2——Linear Regression_第2张图片](http://img.e-com-net.com/image/info5/b5c87e955b3a408ea5dd58a2f5685946.jpg)
![[置顶] 【机器学习笔记3】Stanford公开课Exercise 2——Linear Regression_第3张图片](http://img.e-com-net.com/image/info5/4723dfd40d56482e9df9fa7f946e6473.jpg)
![[置顶] 【机器学习笔记3】Stanford公开课Exercise 2——Linear Regression_第4张图片](http://img.e-com-net.com/image/info5/c413ef26a71e48f4923c3e657c832e53.jpg)
![[置顶] 【机器学习笔记3】Stanford公开课Exercise 2——Linear Regression_第5张图片](http://img.e-com-net.com/image/info5/73bc675382694c679a430b7f2a91b705.jpg)
![[置顶] 【机器学习笔记3】Stanford公开课Exercise 2——Linear Regression_第6张图片](http://img.e-com-net.com/image/info5/631cd9849177443fac8bbc5d44fb5de8.jpg)
![[置顶] 【机器学习笔记3】Stanford公开课Exercise 2——Linear Regression_第7张图片](http://img.e-com-net.com/image/info5/7162f297accd477eaa9a1f8b5293753b.jpg)