凸包算法
其实这个算法是在一年前得某场比赛中临时抱佛脚学的,今天重新的来温习了一遍
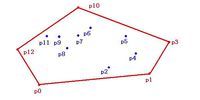
如何来理解凸包?一组平面上的点,求一个包含所有点的最小的凸多边形,这就是凸包问题了。这可以形象地想成这样:在地上放置一些不可移动的木桩,用一根绳子把他们尽量紧地圈起来,这就是凸包了,百度百科中的这张图很生动+活泼+形象,所以你懂的
好说完这个我们首先要来了解下极角排序和左转判定
极角排序:就是选取一个最左的点,按y最小,其次x最小来定义,接下来所有的点针对该点的射线,
按角度由小到大,若相同按距离由近到远来排序
左转判定:这个和叉积有关,对于向量p1(x1,y1),p2(x2,y2)如果x1*y2-x2*y1>0,则从p1到p2左转
我学的是Graham算法,那么接下来来介绍下该算法
(1)选取最下左的点P0
(2)计算出每个点相对于P0的角度和距离(利用这个来排序)排序
(3)设点数为n,将p[n-1]和p[0]入栈,判断点集合是否为一条直线(初始k=2表示当前凸包的大小)
(4)i从1到n-1遍历,对于p[k-1],p[k-2],p[i]若满足左转,将p[i]压入栈
否则i--,k--
(5)k--,返回k表示凸包的点数
下面是我写的模板
int Polygon::Graham(Polygon &con){//别用自己做对象 int t=0,i; Point tmp; //先y最小再x最小 for(i=1;i<n;i++)if(p[i]<p[t])t=i; swap(p[t],p[0]); for(i=0;i<n;i++){ tmp=p[i]-p[0]; p[i].dis=tmp.Len2(); p[i].angle=atan2(tmp.y,tmp.x); } sort(p,p+n,_cmp); //for(int i=0;i<n;i++)p[i].out(); //cout<<"***"<<endl; int k=0; con.p[k++]=p[n-1]; con.p[k++]=p[0]; if(Sig(p[1].angle-p[n-1].angle)==0)con.p[k++]=p[n-1];//凸包为一线段 else{ for(i=1;i<n;i++){ //con[k-1].out(); //con[k-2].out(); //p[i].out(); if(Sig(Cross(con.p[k-1],con.p[k-2],p[i]))>0)con.p[k++]=p[i]; else {i--;k--;} //cout<<"---"<<endl; //for(int j=0;j<k;j++)con[j].out(); //system("pause"); } } return con.n=--k; } /* 9 1 4 3 6 5 7 2 2 3 3 5 4 8 3 9 6 7 1 */
正在学习Melkman算法中。。。