ZOJ 3470 Magic Squares

Magic Squares Time Limit: 2 Seconds       Memory Limit: 65536 KB

One day, the astronauts from China arrived in a planet that they have never been before. First, they sent a robot called AAA to explore the environment as usual.

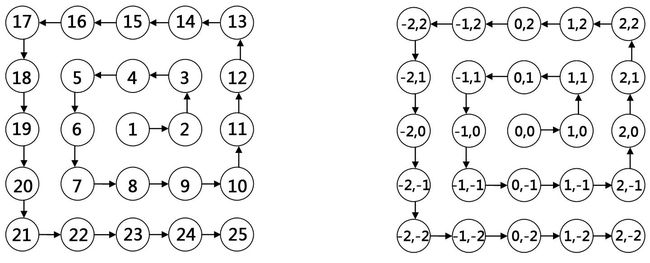
However, AAA became confused as soon as it departed from the aerostat: it found that the surface of the planet was divided into many blocks we call magic squares, each block is marked by an unique integer in a special order(as shown in the left graph). Fortunately, AAA is so clever that it soon found the relationship between these blocks and the Descartes coordinate system (as shown in the right graph).

Before each movement, AAA would send its current block number to the monitor, then move to the right position the monitor order it to. Assuming that the monitor would only order AAA to move to the block neighbored to the current block. We say two blocks are neighbor if they share one same edge.

To complete the task in time, the monitor need to respond to the request of the robot as soon as possible. But the computing progress may be too complicated for beings. So they now turn to you, an excellent programmer, help them list the blocks the AAA can reach at the time in order to sent command to the robot in a short time.

Input

The first line of input is the number of test cases T, then T lines follow, each is a test case with only one positive integers n no larger than 2,000,000,000.

Output

The output consists of exactly T lines, one line for each case.
Line i (1 <= i <= T) should contain an increasing sequence of integers separated by single spaces -- the numbers of the blocks that the robot could reach (with its current block numbered n).

Sample Input

1
5

Sample Output

4 6 16 18

先判断数字所处的层数，然后分8种情况（在四个拐角处或是在四条边上）来推往里或往外一层的相邻的两个数字（因为四个数字中一定有两个是比其小1和大1的数字其他两数字是不同层的，需要分情况讨论），最后可以将8种情况整理成4种情况进行编写 ~

代码如下：

#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>

using namespace std;

int save[5];

void s_save(int x, int y, int m, int n)
{
    save[0] = x;
    save[1] = y;
    save[2] = m;
    save[3] = n;
}

int dif(int num, int i, int dig, int d)
{
    if(num < dig)
    {
        s_save(num - d + 8 - 2 * i,num - 1,num + 1,num + d + 2 * i);
        return 1;
    }
    else if(num == dig)
    {
        s_save(num - 1, num + 1, num + d + 2 * i, num + d + 2 * (i + 1));
        return 1;
    }
    return 0;
}

void solve(int num, int cov, int dig, int d)
{
    int flag = 0;
    dig += cov;
    flag = dif(num, 0, dig, d); //从上 边开始推
    if(!flag)  //判断是否在左 边上
    {
        dig += cov * 2;
        flag = dif(num, 1, dig, d);
    }
    if(!flag)  //判断是否在下 边上
    {
        dig += cov * 2 + 1;
        flag = dif(num, 2, dig, d);
    }
    if(!flag)  //判断是否在右 边上
    {
        dig += cov * 2 + 1;
        flag = dif(num, 3, dig, d);
    }
    if(!flag)  //判断是否在转完一圈的 上边上
    {
        s_save(num - d,num - 1,num + 1,num + d + 8);
    }
}

void find_cov(int num) //确定元素所在层数
{
    int d = 3, cov = 0, dig = 1;
    while(1)
    {
        if(cov)
            d += 8;
        dig += d;
        if(num <= dig)
            break;
        ++cov;
    }
    if(num == 1)
        s_save(2,4,6,8);
    else
        solve(num, cov, dig - d, d);
}

int main()
{
#ifdef test
    freopen("in.txt", "r", stdin);
#endif
    int t, num;
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d", &num);
        find_cov(num);
        printf("%d %d %d %d\n",save[0],save[1],save[2],save[3]);
    }
    return 0;
}