概率随机问题【3】给定能随机生成1到5的函数，写出能随机生成1到7的函数

概率随机问题【1】相关C语言知识：http://blog.csdn.net/hxz_qlh/article/details/12843131

概率随机问题【2】 取样与概率：http://blog.csdn.net/hxz_qlh/article/details/12877465

随机算法涉及大量概率论知识，本文总结最常见的一些随机算法的题目。

已知随机函数rand(),以p的概率产生0，以1-p的概率产生1，现在要求设计一个新的随机函数newRand(), 使其以1/n的等概率产生1~n之间的任意一个数。

1. 解决思路：可以通过已知随机函数rand()产生等概率产生0和1的新随机函数Rand()，然后调用k（k为整数n的二进制表示的位数）次Rand()函数，得到一个长度为k的0和1序列，以此序列所形成的整数即为1--n之间的数字。注意：从产生序列得到的整数有可能大于n，如果大于n的话，则重新产生直至得到的整数不大于n。
   第一步：由rand()函数产生Rand()函数，Rand()函数等概率产生0和1。
   

    int Rand()
    {
        int i1 = rand();
        int i2 = rand();
        if(i1==0 && i2==1)
            return 1;
        else if(i1==1 && i2==0)
            return 0;
        else
            return Rand();
        return -1;
    }

   第二步：计算整数n的二进制表示所拥有的位数k，k = 1 +log2n（log以2为底n）
   第三步：调用ｋ次Rand()产生随机数。

    int newRand()
    {
        int result = 0;
        for(int i = 0 ; i < k ; ++i)
        {
            if(Rand() == 1)
                result |= (1<<i);
        }
        if(result > n)
            return newRand();
        return result;
    }

   给定rand5()能随机生成整数1到5的函数,写出能随机生成整数1到7的函数rand7()
   思路：
   很多人的第一反应是利用rand5() + rand5()%3来实现rand7()函数，这个方法确实可以产生1-7之间的随机数，但是仔细想想可以发现数字生成的概率是不相等的。rand()%3 产生0的概率是1/5，而产生1和2的概率都是2/5，所以这个方法产生6和7的概率大于产生5的概率。正确的方法是利用rand5()函数生成1-25之间的数字，然后将其中的1-21映射成1-7，丢弃22-25。例如两次rand5()分别生成(1，1)，则看成rand7()中的2，如果出现22,23,24,25，则丢弃重新生成。
   简单实现：

    int rand7()
    {
        int x = 0;
        do
        {
            x = 5 * (rand5() - 1) + rand5();
        }while(x > 21);
        return 1 + x%7;
    }

   我的备注：
2.     这种思想是基于，rand()产生[0,N-1]，把rand()视为N进制的一位数产生器，那么可以使用rand()*N+rand()来产生2位的N进制数，以此类推，可以产生3位，4位，5位...的N进制数。这种按构造N进制数的方式生成的随机数，必定能保证随机，而相反，借助其他方式来使用rand()产生随机数(如 rand5() + rand()%3 )都是不能保证概率平均的。
       此题中N为5，因此可以使用rand5()*5+rand5()来产生2位的5进制数，范围就是1到25。再去掉22-25，剩余的除3，以此作为rand7()的产生器。

   给定一个函数rand()能产生0到n-1之间的等概率随机数，问如何产生0到m-1之间等概率的随机数？
   

    int random(int m , int n)
    {
        int k = rand();
        int max = n-1;
        while(k < m)
        {
            k = k*n + rand();
            max = max*n + n-1;
        }
        return k/(max/n);
    }

   如何产生如下概率的随机数？0出1次，1出现2次，2出现3次，n-1出现n次？

    int random(int size)
    {
        while(true)
        {
            int m = rand(size);
            int n = rand(size);
            if(m + n < size)
                return m+n;
        }
    }

3. 趣味概率题

   1）生男生女问题：在重男轻女的国家里，男女的比例是多少？在一个重男轻女的国家里，每个家庭都想生男孩，如果他们生的孩子是女孩，就再生一个，直到生下的是男孩为止。这样的国家，男女比例会是多少？

   答案：还是1：1。在所有出生的第一个小孩中，男女比例是1：1；在所有出生的第二个小孩中，男女比例是1：1；.... 在所有出生的第n个小孩中，男女比例还是1：1。所以总的男女比例是1：1。

   为了验证我的判断，我写了个程序，模拟100000对夫妇，执行结果和我想象的完全相同：男女比例1:1！我抽样看了一下，有好几对“模拟夫妇”连着生了14个女儿才生出一个儿子来，瀑布汗！

   程序如下，有兴趣的同学可以自己运行一下，用0代表女儿，用1代表儿子。最后一行显示儿子和女儿的数量。

   int girl = boy = 0;
   for(int i = 0; i < 100000; i ++) {
   	while(!rand(0, 1)) {
   	    cout<< '0';
   	    girl ++;
   	}
   	boy ++;
   	cout<< '1';
   }
   

   只要男女出生概率一样，那么无论怎么变着花样生，只要不生下来就掐死，样本越大，肯定越接近1:1，因为每个孩子出生男女概率是50%，所以每次出生的男女比例是相同的。假设这个国家有n对夫妇，那么n对夫妇将生下n个男孩，这n个男孩是这样生下的，假设生男生女的概率是50%，那么n/2个男孩是第一胎生下的，同时将有 n/2个女孩生下，n/2对生女孩的夫妇将继续生，其中n/4的夫妇生下男孩，n/4的夫妇继续生下女孩，然后是n/8的夫妇顺利得到男孩，又有n/8的夫妇生下女孩，依此类推，这个国家将生下n/2 + n/4 + n/8 + ...的女孩，所以男女比例是n : (n/2 + n/4 + n/8 + ...) = n : n = 1 : 1
   

   
   

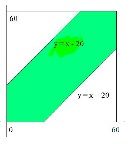
   2）约会问题：两人相约5点到6点在某地会面，先到者等20分钟后离去，求这两人能够会面的概率。

   答案：设两人分别在5点X分和5点Y分到达目的地，则他们能够会面的条件是|X-Y| <= 20，而整个范围为S={(x, y): 0 =< x <= 60,  0=< y <= 60}，所以会面的情况为图中表示的面积，概率为(60^2 - 40^2) / 60^2 = 5/9。

   

   3）帽子问题：有n位顾客，他们每个人给餐厅的服务生一顶帽子，服务生以随机的顺序归还给顾客，请问拿到自己帽子的顾客的期望数是多少？

   答案：使用指示随机变量来求解这个问题会简单些。定义一个随机变量X等于能够拿到自己帽子的顾客数目，我们要计算的是E[X]。对于i=1, 2 ... n，定义Xi =I {顾客i拿到自己的帽子}，则X=X1+X2+...Xn。由于归还帽子的顺序是随机的，所以每个顾客拿到自己帽子的概率为1/n，即Pr(Xi=1)=1/n，从而E(Xi)=1/n，所以E(X)=E(X1+X2+...Xn)=E(X1)+E(X2)+...E(Xn)=n*1/n = 1。即大约有1个顾客可以拿到自己的帽子。
   

   4）生日悖论：一个房间至少要有多少人，才能使得有两个人的生日在同一天？
   答案：对房间k个人中的每一对(i, j)定义指示器变量Xij = {i与j生日在同一天} ，则i与j生日相同时，Xij=1，否则Xij=0。两个人在同一天生日的概率Pr(Xij=1)=1/n。则用X表示同一天生日的两人对的数目，则E(X)=E(∑^k_i=1 ∑^k_j=i+1 Xij) = C(k,2)*1/n = k(k-1)/2n，令k(k-1)/2n >=1， 可得到k>=28，即至少要有28个人，才能期望两个人的生日在同一天。
   

   5）如果在高速公路上30分钟内看到一辆车开过的几率是0.95，那么在10分钟内看到一辆车开过的几率是多少？(假设常概率条件下)

   答案：假设10分钟内看到一辆车开过的概率是x，那么没有看到车开过的概率就是1-x，30分钟没有看到车开过的概率是(1-x)^3，也就是0.05。所以得到方程(1-x)^3 = 0.05 ，解方程得到x大约是0.63。 

   
   

   参考资料：
4. 1、http://www.cnblogs.com/yysblog/archive/2012/06/27/2566276.html
5. 2、http://blog.csdn.net/sgbfblog/article/details/7917685
6.